
Standart sapma, formül ya da ne adlandırılan standart sapma açıklamak için kullanılan istatistiksel bir teknik olan bir grup homojenliğini.
Standart sapma, verilerin bir örneklem içinde nasıl dağıtıldığını ve ayrıca tek tek noktalar ile örneğin ortalama veya ortalama değeri arasındaki ilişkiyi açıklamak için de kullanılabilir .
Daha fazla tartışmadan önce bilmemiz gereken birkaç şey var, yani nerede:
Veri setinin standart sapması sıfır olabilir veya sıfırdan büyük veya küçük olabilir.
Bu değişen değerler aşağıdaki anlamlara sahiptir:
- Standart sapma sıfırsa, veri setindeki tüm örnek değerler eşittir.
- Bu arada sıfırdan büyük veya küçük standart sapma değeri, bireyin veri noktasının ortalama değerden uzak olduğunu gösterir.

Standart sapmayı bulma adımları
Standart sapma değerini belirlemek ve bulmak için aşağıdaki adımları izlememiz gerekir.
- İlk adım
Her veri noktasındaki ortalama veya ortalama değeri hesaplayın.
Bunu, veri kümesindeki her bir değeri ekleyerek yaparsınız, ardından sayı, verilerden elde edilen toplam nokta sayısına bölünür.
- Sonraki adım
Her veri noktası için ortalama değerden sapmayı veya farkı hesaplayarak verilerin varyansını hesaplayın.
Her veri noktasındaki sapma değerinin karesi alınır ve ortalama değerin karesiyle çıkarılır.
Varyans değerini elde ettikten sonra varyans değerini köklendirerek standart sapmayı hesaplayabiliriz.
Ayrıca şunu okuyun: Anlatım: Tanım, Amaç, Özellikler, Türler ve ÖrneklerStandart Sapma Formülleri
1. Nüfus Standart Sapması
Bir popülasyon, σ (sigma) ile sembolize edilir ve aşağıdaki formülle tanımlanabilir:

2. Standart Örnek Sapması
Formül şudur:
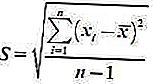
3. Birçok veri grubunun standart sapması için formül
Bir örnekten veri dağılımını bulmak için her bir veri değerini ortalama değere indirebiliriz, ardından tüm sonuçlar eklenir.
Bununla birlikte, yukarıdaki yöntemi kullanırsanız sonuç her zaman sıfır olacaktır, bu nedenle bu yöntem kullanılamaz.

Sonuç sıfır (0) olmaması için, o zaman önce veri değerindeki düşüşün ve ortalama değerin karesini almalı, sonra tüm sonuçları toplamalıyız.
Bu yöntemi kullanarak , kareler toplamının sonucu pozitif bir değere sahip olacaktır.

Varyans değeri, kareler toplamının veri boyutu sayısına (n) bölünmesiyle elde edilecektir.
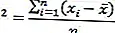
Bununla birlikte, popülasyonun varyansını bulmak için varyans değerini kullanırsak varyans değeri, örnek varyanttan daha büyük olacaktır.
Bunun üstesinden gelmek için, bölücü olarak veri boyutu (n) , örnek varyans değerinin popülasyon varyantına yaklaşması için serbestlik dereceleri (n-1) ile değiştirilmelidir .
Böylece , örnek varyant formülü şu şekilde yazılabilir:

Elde edilen varyantın değeri kare değeridir, bu nedenle standart sapmayı elde etmek için önce karesini almamız gerekir.

Hesaplamayı kolaylaştırmak için varyans ve standart sapma formülü aşağıdaki formüle indirgenebilir.
Veri varyantı formülleri
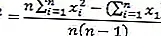
Standart sapma formülü
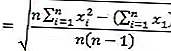
Açıklamalar :
s2 = değişken
s = standart sapma
x i = ith x değeri
n = örnek boyutu
Standart Sapma Problemlerine Örnek
Aşağıdaki bir örnektir ve standart sapma problemleri üzerinde çalışmaktadır.
Soru:
Sandi, müfredat dışı üyelerin başkanı olarak üyelerin toplam boylarını kaydetme görevine sahiptir. Şifre ile toplanan veriler aşağıdaki gibidir:
167, 172, 170, 180, 160, 169, 170, 173, 165, 175
Yukarıdaki verilerden standart sapmayı hesaplayın!
Ayrıca şunu okuyun: Mors Kodu: Tarih, Formüller ve Ezberleme YöntemleriCevap :
| ben | x ben | x ben 2 |
| 1 | 167 | 27889 |
| 2 | 172 | 29584 |
| 3 | 170 | 28900 |
| 4 | 180 | 32400 |
| 5 | 160 | 25600 |
| 6 | 169 | 28561 |
| 7 | 170 | 28900 |
| 8 | 173 | 29929 |
| 9 | 165 | 27225 |
| 10 | 175 | 30625 |
| Σ | 1710 | 289613 |
Yukarıdaki verilerden, veri sayısının (n) = 10 ve serbestlik derecesinin (n-1) = 9 olduğu da görülebilir.
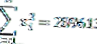
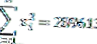
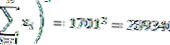
Böylece varyans değerini aşağıdaki gibi hesaplayabiliriz:

Sandi'nin topladığı verilerin değişken değeri 30,32'dir . Standart sapmayı hesaplamak için sadece varyans değerinin karesini almamız gerekir, böylece:
s = √30.32 = 5.51
Yani yukarıdaki problemin standart sapması 5.51'dir.
Avantajlar ve uygulamalar
Standart sapma, alınan verilerin tüm popülasyonu temsil edip etmediğini belirlemek için istatistikçiler tarafından yaygın olarak kullanılır.

Örneğin, bir köydeki 3-4 yaş arası bir bebeğin kilosunu öğrenmek isteyen biri.
Bu yüzden kolaylaştırmak için sadece birkaç çocuğun ağırlığını bulmamız ve ardından ortalama ve standart sapmayı hesaplamamız gerekiyor.
Ortalama ve standart sapma değerlerinden, bir köydeki 3-4 yaş arası çocukların tüm vücut ağırlıklarını temsil edebiliriz.
Referans
- Standart Sapma - Nasıl Bulunacağına İlişkin Formüller ve Sorun Örnekleri
- Standart Sapma: Hesaplama Formülleri ve Örnek Problemler
