
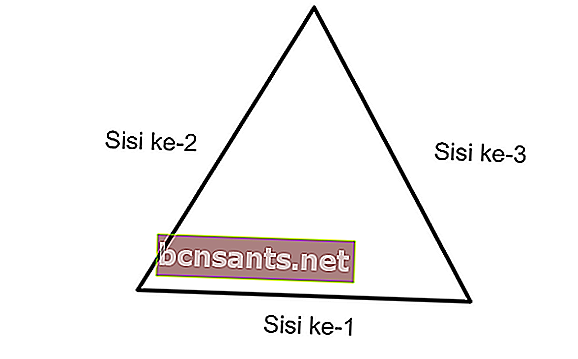
Üçgenin çevresi, üçgenin kenarının toplam uzunluğudur. Bu nedenle, üçgenin çevresi için formül K = a + b + c veya üçgenin tüm kenarlarının toplamıdır.
Üçgen bahçenin etrafında döndüğünüzde, bu ne anlama geliyor? Evet! Üçgen bir şeklin etrafında dönüyorsunuz. Düz üçgen şekli nedir? Aşağıda, üçgenin açıklaması, üçgenin türü ve üçgenin çevresinin nasıl belirleneceği veya formülü yer almaktadır.
Üçgen Açıklama
Üçgen, bir açı oluşturan üç kesişen çizgiden oluşan bir şekildir. Bir üçgendeki açı sayısı 180 derecedir.
Üçgenler, en basit düz şekillerdir çünkü bunlar, prizmalar ve piramitler gibi şekilleri oluşturan kareler, dikdörtgenler, daireler ve düz şekillerin öğeleri gibi diğer düz şekilleri oluşturan öğelerdir.
Üçgenin Özellikleri
Bir üçgenin anlamını daha fazla açıklamak için, aşağıda ABC şeklinde rastgele bir üçgen şekli çizeceğim:
ABC üçgenindeki öğeler şunları içerir:
- A, B ve C noktaları köşeler olarak bilinir.
- AB, BC ve CA çizgilerine üçgenin kenarları denir.
- Üçgenin oluşturduğu yan uzunluklardan ve açılardan çeşitli üçgenler görülebilir.
Üçgen Türleri
Üçgen türleri, üçgeni oluşturan kenarların ve açıların uzunluğuna bağlı olarak büyük ölçüde değişir. Aşağıdaki üçgen türlerinin bölünmesidir
Kenar uzunluklarına göre üçgen türleri
- Eşkenar üçgen
Yani üç kenarı da aynı uzunlukta olan bir üçgen. Ayrıca yan üçgenin oluşturduğu üç açı aynı boyuttadır, yani 60 derece, çünkü üçgenin açı sayısı 180 derecedir.
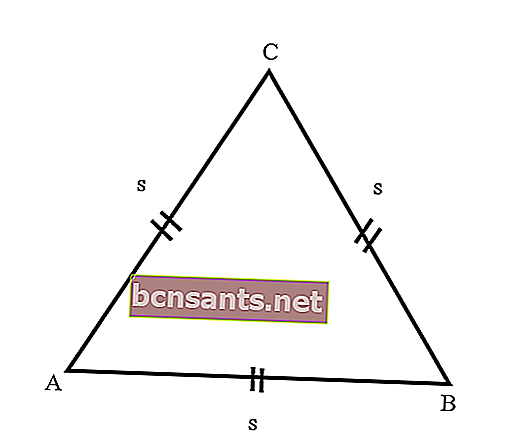
Eşkenar üçgenler hakkında daha fazla bilgi edinmek için, eşkenar üçgenlerin özelliklerinin aşağıdaki açıklamasını dikkate alın:

Şekil (b) - (d) 'de, ABC üçgeninin şeklinin çerçevesini tam olarak 3 yol kullanarak kaplayabildiği görülmektedir, yani, O noktasında ortalanmış olarak 120 dereceye kadar döndürülmüş (dönme yönüne bakınız) (Şekil b) dönüş merkezinde 240 dereceye kadar döndürülmüştür. O noktasında (şekil d) merkez noktasında 360 derece (bir tam dönüş) döndürülen O noktasında (şekil c).
Ayrıca şunu okuyun: Fırsat Formülleri ve Sorun ÖrnekleriŞekil a'dan f'ye kadar olan şekillerin açıklamasına göre, ABC eşkenar üçgeni 3. seviyeye kadar dönme simetrisine sahiptir. Bu arada, ters çevrilmiş e, f ve g şekilleri çerçeveyi doğru şekilde işgal edebilir. Bunun için ABC üçgeninin şekli 3 eksen simetriye sahiptir. Yukarıdaki resimde ise, simetri eksenleri CD, BF ve AE'dir. Böylece eşkenar üçgen çerçeveyi tam olarak 6 şekilde işgal edebilir.
Yukarıdaki açıklamalardan bazılarına dayanarak, bir eşkenar üçgende bulunan özelliklerden bazıları şunlardır: 3 seviyeli dönme simetrisi, 3 ekseni simetri, 3 eşit kenar, 3 eşit 60 derece açıya sahiptir ve çerçeveyi 6 yola kadar işgal edebilir.
- İkizkenar üçgen
Yani bir kenarı aynı uzunlukta olan bir üçgen. Bir ikizkenar üçgenin iki eşit açısı vardır, yani birbirine bakan açıları.
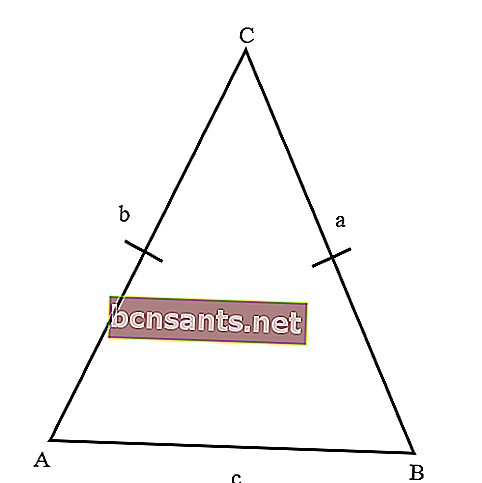
Aşağıdakiler ikizkenar üçgenin özellikleridir;
- Bir ikizkenar üçgen oluşturmak, onu bir tam dönüş için döndürmek, çerçeveyi tam olarak tek bir şekilde kaplar. Böylece samakaki üçgeni bir döner simetriye sahiptir.
- Bu arada, bir ikizkenar üçgenin yalnızca bir simetri ekseni vardır.
- Herhangi bir üçgen
Yani üç kenarı aynı uzunlukta olmayan ve üç açı eşit olmayan bir üçgen.

İşte herhangi bir üçgenin özellikleri:
- Aynı uzunlukta olmayan üç kenarı vardır. (Yukarıdaki resimde üç kenarın uzunluğu BA ≠ CB ≠ AC olmalıdır).
- Kıvrım simetrisi yoktur.
- Yalnızca bir dönen simetriye sahiptir.
- Üç köşenin farklı boyutları vardır.
Açıya göre üçgen türleri
- Dar üçgen
Yani, dar bir açı oluşturan üç açılı bir üçgen. Dar açı, 0 ila 90 derece arasında değişen bir açıdır.
- Künt üçgen
Yani bir köşesi geniş bir açı oluşturan bir üçgen. Geniş açı, büyüklüğü 90 ila 180 derece aralığında olan bir açıdır.
Ayrıca şunu okuyun: Sıklıkla Unutulan Formüller için Çözümler!
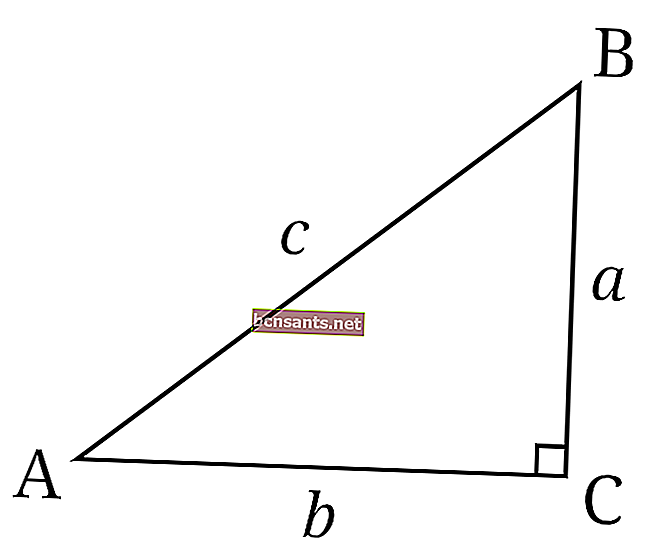
- Dik üçgen
Yani, köşelerinden birinin 90 derecelik bir açı oluşturduğu bir üçgen.
Bir üçgenin çevresi için formül
Şeklin çevresi, şekli oluşturan kenarların (kenarların) uzunluklarının sayısından elde edilir.
Böylece, bir üçgenin çevresi için formül, üçgenin her bir kenarını toplayarak elde edilebilir.
Üçgenin çevresi = 1. tarafın uzunluğu + 2. tarafın uzunluğu + 3. tarafın uzunluğu
K = a + b + c
Bir Üçgenin Çevresini Bulmada Örnek Problem
Örnek Problem 1.
Eşkenar üçgenin kenar uzunluğu 3 cm, çevresi nedir!
Yerleşme:
Bilirsiniz: s = 3 cm
Aranıyor: Üçgenin çevresi mi?
Cevap:
Eşkenar üçgenlerin aynı tarafları vardır,
K = s + s + s
K = 3 + 3 + 3
K = 9 cm
Yani, eşkenar üçgenin çevresi 9 cm'dir.
Örnek Problem 2.
Bir ikizkenar üçgenin toplam yan uzunluğu 36 cm'dir. En uzun kenar 13 cm'dir. En kısa kenarın uzunluğu nedir?
Yerleşme:
Biliyorsunuz = K = 36 cm; b = a = 13 cm
Aranan : En kısa kenarın uzunluğu?
Cevap :
Üçgenin çevresi = a + b + c
36 = 13 + 13 + c
c = 10 cm
Yani üçgenin en kısa kenar uzunluğu 10 cm
Örnek Problem 3.
Kenarları 9, 11, 13 cm olan rastgele bir üçgeniniz var. Üçgenin çevresini hesaplayın!
Yerleşme:
Bilindiği gibi : a = 13 cm; b = 9 cm; c = 11cm
Aranıyor : Üçgenin çevresi mi?
Cevap:
K = a + b + c
K = 13 +9 +11
K = 33 cm
Yani üçgenin çevresi 33 cm
Örnek problem 4.
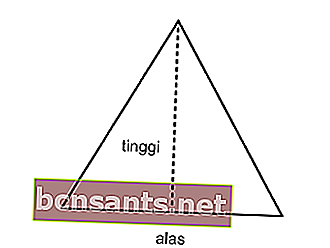
12 cm2 alana ve 6 cm yan uzunluğa sahip ikizkenar üçgenin çevresini hesaplayın!
Yerleşme:
Bilirsiniz: L = 12 cm2; a = 6 cm
Aranıyor: Üçgenin çevresi mi?
Cevap:
Üçgenin çevresini bulmak için, üçgenin kenarlarının uzunluğunu bilmeniz gerekir.
Üçgenin yüksekliğini bulmak için alanı kullanın
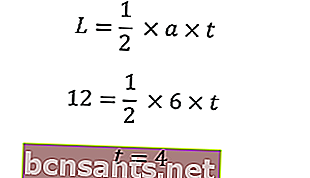
Pisagor sistemini kullanarak, tabanın uzunluğunu (a) ve üçgenin (t) yüksekliğini girerek bir ikizkenar üçgenin hipotenüsünü biliyoruz.

Yukarıdaki denklemi kullanarak üçgenin hipotenüsünü elde ederiz.
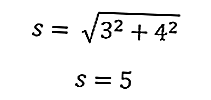
Bu, üçgenin çevresini hemen hesaplamanıza izin verecektir.
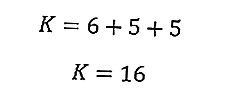
Yani üçgenin çevresi 16 cm
Referans : Üçgen - Matematik Eğlencelidir
