
Alan inşa etmek matematikte sıklıkla tartışılan bir konudur, formül genellikle ilkokul ve ortaokul seviyelerinde bir matematik problemidir.
Bina alanı, matematiksel olarak hacmi veya içeriği olan bir bina olarak yorumlanabilir. Bir mekanın şeklinin, hacmi veya alanı olan ve kenarlarla sınırlı üç boyutlu bir şekil olduğu da yorumlanabilir.
Bloklar, küpler, tüpler, toplar vb. Gibi çeşitli uzay biçimleri vardır.
Bu şekillerin her birinin sırasıyla hacim ve yüzey alanı için bir formülü vardır. Bu bazen birçok öğrencinin hatırlamasını zorlaştırır.
Aşağıda, bu konudaki çeşitli matematik problemlerini kolayca çözebilmeniz için bina formüllerinin tam bir listesini yaptım.
1. Küp
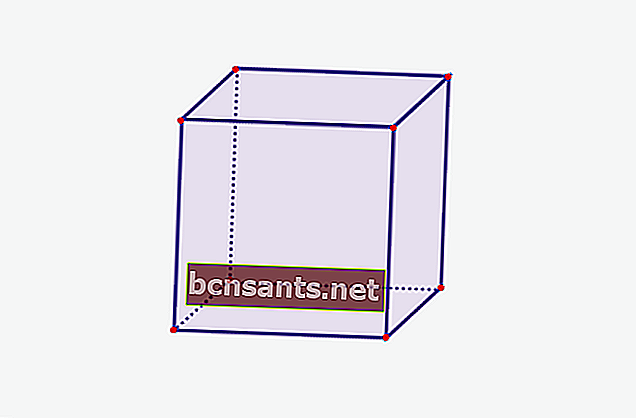
| Küp hacmi | V = sxsxs |
| Küpün yüzey alanı | L = 6 x (sxs) |
| Küpü daire içine alın | K = 12 xs |
| Bir tarafın alanı | L = sxs |
2. Kirişler
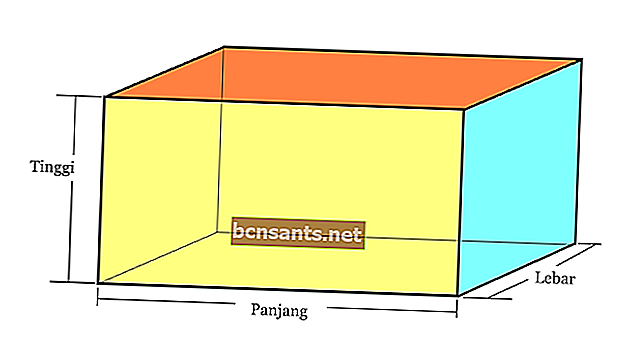
| Blok hacmi | V = pxlxt |
| Yüzey alanını engelle | L = 2 x (pl + lt + pt) |
| Çapraz boşluk | d = √ ( p2 + l2 + t2) |
| Işının çevresi | K = 4 x (w + l + h) |
3. Üçgen Prizma
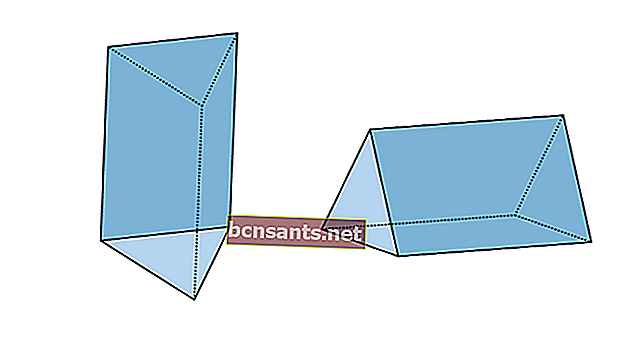
| Üçgen prizmanın hacmi | V = xt tabanının alanı |
| Üçgen prizmanın yüzey alanı | L = taban xt + 2 x üçgenin tabanının çevresi |
4. Beşinci Dörtgen
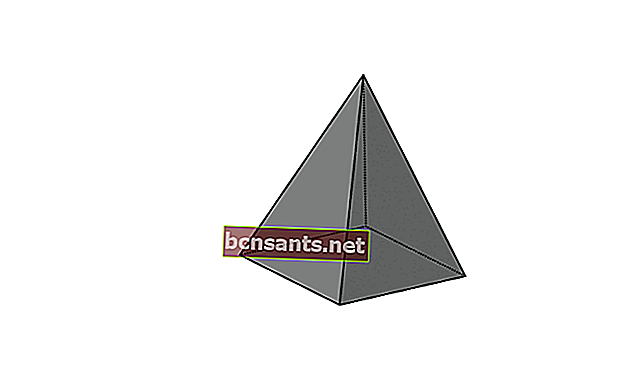
| Piramidin hacmi | V = 1/3 xpxlxt |
| Piramidin yüzey alanı | L = taban alanı + piramit kasasının alanı |
5. Beşinci Üçgen
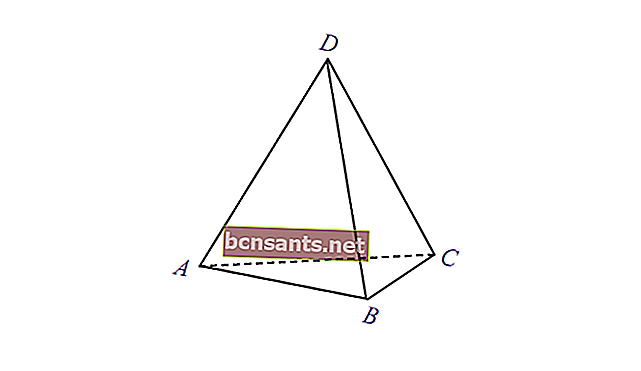
| Piramidin hacmi | V = 1/3 x xt tabanının alanı |
| Yüzey alanı | L = taban alanı + piramit kasasının alanı |
6. Tüpler

| Tüp hacmi | V = π x r2 xt |
| Tüp yüzey alanı | L = (2 x taban alanı) + (tabanın çevresi x yükseklik) |
7. Koniler

| Koni hacmi | V = 1/3 x π x r2 xt |
| Koninin yüzey alanı | Bir = (π x r2) + (π xrxs) |
8 top

| Top hacmi | V = 4/3 x π x r3 |
| Topun yüzey alanı | Bir = 4 x π x r2 |
Yapı formüllerinin tam tablosu
Aşağıdaki tabloya bakarak da kısaca yukarıdaki listeye ulaşabilirsiniz. İstediğiniz zaman yeniden görebilmek için bu resmi de kaydedebilirsiniz.
Bu, hacim ve yüzey alanını hesaplamak için bina formu formülünün bir açıklamasıdır.
Umarım yukarıdaki açıklama uzayın şeklini anlamanıza yardımcı olabilir, böylece onu matematik problemlerini ve günlük yaşamdaki çeşitli uygulamalarını çözmek için kullanabilirsiniz.
Referans
- Hacim formülleri incelemesi - Khan Academy
- Geometri Formül Sayfası
