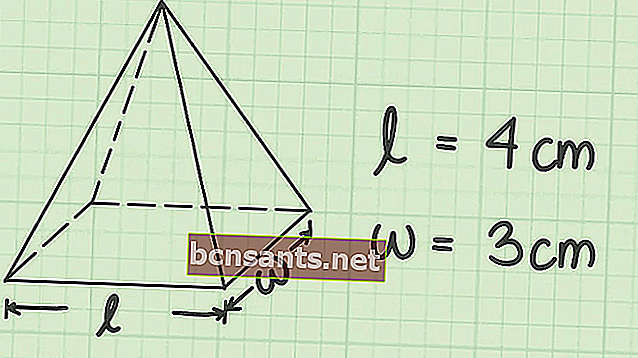
Piramidin hacmi = 1/3 x Taban alanı x Yükseklik . Bu durumda, piramidin taban alanı için formül, onu oluşturan şeklin şekline bağlıdır. Detaylar bu makalede tartışılmaktadır.
Limas , tepesinde bir tepe noktası olan üçgen dikey kenarlara sahip çok taraflı bir tabana sahip bir yapıdır.
Bina alanı, piramidin yanı sıra kendi özelliklerine de sahiptir. İşte bir piramit odasının özellikleri.
- Piramidin üst düzlemi keskin bir noktadır
- Piramidin alt düzlemi bir şekildir
- Piramidin yan düzlemi üçgendir
Limas Elemanları
Diğer yapı taşlarına benzer şekilde, piramit aşağıdakileri içeren unsurlardan oluşur:
- Köşe noktası
- Yanal
- Yan düzlem
Bir piramit, çeşitli uzay şekillerinden oluştuğu için, her bir şeklin, piramit şeklinin şekline göre değişen bir dizi öğesi vardır.
Limas Türleri
Limas, tabanın şekline bağlı olarak çeşitli alan biçimlerine sahiptir.
1. Üçgen piramit
Bu, tabanı eşkenar, ikizkenar veya herhangi bir üçgen olan bir üçgen olan bir piramit türüdür.
Üçgen piramit öğesi:
- 4 köşe noktası
- 4 yan düzlem
- 6 kaburga

2. Beşinci Kareler
Tabanı dikdörtgen (kare, dikdörtgen, uçurtma, eşkenar dörtgen, paralelkenar, yamuk ve diğer dikdörtgen şekiller) olan bir piramit türüdür.
Dikdörtgen piramit öğesi:
- 5 köşe noktası
- 5 yan düzlem
- 8 kaburga

3. Lias Beş Puan
İster normal bir beşgen, ister herhangi bir beşgen olsun, beşgen düz bir tabanı olan bir piramit türüdür.
Beşgen piramidin unsurları:
- 6 köşe noktası
- 6 yan düzlem
- 10 kaburga

4. Beşinci Altıgen
Hem normal altıgen hem de keyfi altıgen şeklinde altıgen taban şekline sahip bir piramit türüdür.
Altıgen piramit öğesi:
- 7 köşe noktası
- 7 yan düzlem
- 12 kaburga

Limas Yüzey Alanı Formülü
Yüzey alanı , bir şekli oluşturan şeklin toplam alanıdır . Bir piramidi oluşturan şekil, tabanın kenarları ve üçgen olan kenarlardan oluşur. Dolayısıyla, genel olarak bir piramidin yüzey alanının formülü aşağıdaki gibidir.
Ayrıca şunu okuyun: İnsan Anatomisi ve İşlevleri + Resimler [TAM]Bir piramidin yüzey alanı formülü = taban alanı + tüm dikey kenarların alanı
Piramit yüzey alanı kavramını daha iyi anlamak için, burada bir piramidin yüzey alanıyla ilgili bir problem örneği verilmiştir.
Örnek Problem 1.
Kenar uzunluğu 10 cm ve piramit yüksekliği 12 cm olan dikdörtgen bir piramit, piramidin yüzey alanı nedir?
Cevap:
Bilinen:
taban alanı = 10 × 10 = 100 cm2
piramit yüksekliği = 12 cm
Aranıyor : piramidin yüzey alanı
Çözüm :
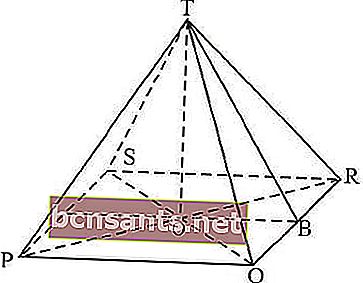
Yüzey alanı = taban alanı + dikey kenarların toplam alanı
taban alanı = yan x yan = 10 x 10 = 100 cm2
dikey kenarın toplam alanı = üçgenin alanı = 4 x QRT üçgeninin alanı
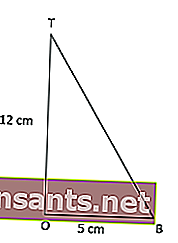
TOB üçgen pisagorunun hesaplanması ile BT yüksekliği 13 cm'dir. yani,
QRT = 1/2 x QR x BT = 1/2 x 10 x 13 = 65 cm2 üçgen alanı
dikey kenarların toplam alanı = 4 x üçgen alanı QRT = 4 x 65 = 260
Yani piramidin yüzey alanı = 100 + 260 = 360 cm2
Örnek Problem 2.
Bir dörtgen için piramidin taban alanının 16 cm2 olduğunu ve dikey üçgenin yüksekliği 3 cm olduğunu biliyorsunuz. Üçgenin piramidinin yüzey alanını bulun.
Cevap.
Bilinir :
piramidin taban alanı = 16 cm2
dikey üçgenin yüksekliği = 3 cm
Aranıyor : Piramidin yüzey alanı
Çözüm :
Piramidin yüzey alanı = taban alanı + dikey tarafın toplam alanı
taban alanı = 16 cm2
dikey toplam alan = 4 x üçgenin alanı = 4 x (1/2 x 4 × 3) = 24 cm2
Yani piramidin yüzey alanı = 16 + 24 = 40 cm2
Örnek Problem 3 .
Düzenli bir altıgen piramidin taban alanı 120 cm2 ve dikey üçgende 30 cm2 alanı vardır. Altıgen piramidin yüzey alanını belirleyin.
Cevap.
Bilinen:
taban alanı = 120 cm2
dikey üçgenin alanı = 30 cm2
Aranıyor : piramidin yüzey alanı
Çözüm :
Yüzey alanı = taban alanı + dikey kenarların toplam alanı
Ayrıca şunu okuyun: İnsanlardaki boşaltım sistemini ve işlevlerini öğrenintaban alanı = 120 cm2
toplam dikey kenar alanı = 6 x dikey üçgen alanı = 6 x 30 cm2 = 180 cm2
Yani, bir altıgen piramidin yüzey alanı = 120 + 180 = 300 cm2
Limas Hacim Formülü
Limas, bir hacme sahip olması için bina alanı içerir. Aşağıdaki genel olarak bir piramidin hacminin formülüdür.
Piramidin hacmi = taban x yüksekliğinin 1/3 x alanı
Bir piramidin hacmini belirleyen örnek problem
Piramit hacim formülünü kullanmayı daha iyi anlamak için, burada bir piramidin hacmini bulmaya yönelik bazı problem örnekleri verilmiştir.
Örnek Problem 1.
Taban alanı 50 cm2 ve piramit yüksekliği 12 cm olan bir yan üçgen piramidin hacmini bulun.
Cevap.
Bilinen:
taban alanı = 50 cm2
piramit yüksekliği = 12 cm
Aranıyor: piramidin hacmi
Çözüm :
Piramidin hacmi = 1/3 x piramidin xt tabanının alanı = 1/3 x 50 x 12 = 200 cm3
Yani piramidin hacmi 200 cm3
Örnek Problem 2.
Kenar uzunluğu 8 cm ve piramit yüksekliği 6 cm olan dikdörtgen bir piramit, piramidin hacmi nedir?
Cevap.
Bilinir :
dikdörtgenin kenarı = 8 cm
piramit yüksekliği = 6 cm
Aranıyor : piramidin hacmi
Çözüm :
Piramidin hacmi = 1/3 x piramidin xt tabanının alanı = 1/3 x (8 x 8) x 6 = 128 cm3
Yani piramidin hacmi 128 cm3'tür.
Örnek Problem 3.
Bir piramidin tabanı 50 cm2 ve piramidin yüksekliği 15 cm olduğu biliniyor, o halde piramidin hacmi nedir?
Cevap.
Biliyorum =
taban alanı = 50 cm2
yükseklik = 15 cm
Sorulan = beşgen piramidin hacmi
Yerleşme.
Hacim = 1/3 x taban alanı x yükseklik
= 1/3 x 50 x 15
= 250 cm3
Yani piramidin hacmi 250 cm3
Böylece, Limas Formülünün tam bir açıklaması: Alan, Hacim, Örnek Sorular + Tartışma. Faydalı olabilir !
