Pascal'ın Üçgen Formülü ve Örnek Problem

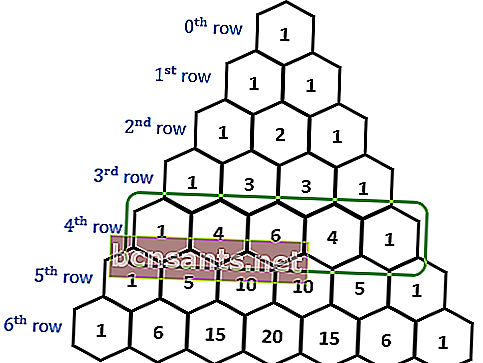
Pascal üçgeni, önceki satıra bitişik öğeler eklenerek oluşturulan bir üçgen düzenlemesidir. Bu üçgen düzeni, önceki satıra bitişik öğeler eklenerek yapılır.

A ve b değişkenlerinin birbirine eklendiğini ve ardından 0'dan 3'ün kuvvetine yükseltildiğini varsayalım, sonuç aşağıdaki tanımdır.

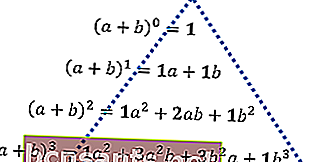
Ardından, üçgen bir şekil bulana kadar sayıların yukarıdan aşağıya doğru kalın harflerle düzenlenmesini düşünün. Bu sayı modeli bundan sonra Pascal üçgeni olarak anılacaktır.

Pascal Üçgenini Anlamak

Pascal üçgeni, bir üçgenin iki terimli katsayısı üzerindeki geometrik kuraldır.

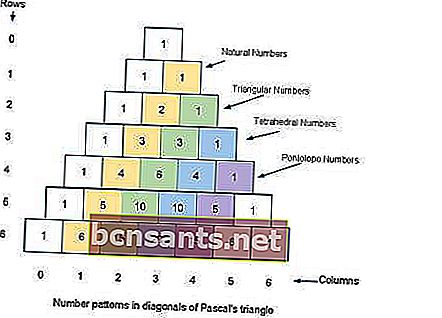
Üçgene matematikçi Blaise Pascal'ın adı verilmiştir, ancak diğer matematikçiler ondan yüzyıllar önce Hindistan, İran, Çin ve İtalya'da çalışmışlardır.

Kural Kavramı

Pascal üçgeni kavramı, a ve b değişkenlerinden bağımsız olarak bu üçgen için bir hesaplama sistemidir. Bu, aşağıdaki gibi binom katsayısına dikkat etmenin yeterli olduğu anlamına gelir:

1. Sıfır satırına sadece 1 rakamını yazın.
2. Aşağıdaki her satıra, her bir sola ve sağa 1 rakamını yazın.
3. Yukarıdaki iki sayının toplamı, ardından aşağıdaki satıra yazılır.
4. (2) 'ye göre solda ve sağda 1 numara, her zaman sonucu (3) çevreler
5. Hesaplamalara aynı desenle devam edilebilir.

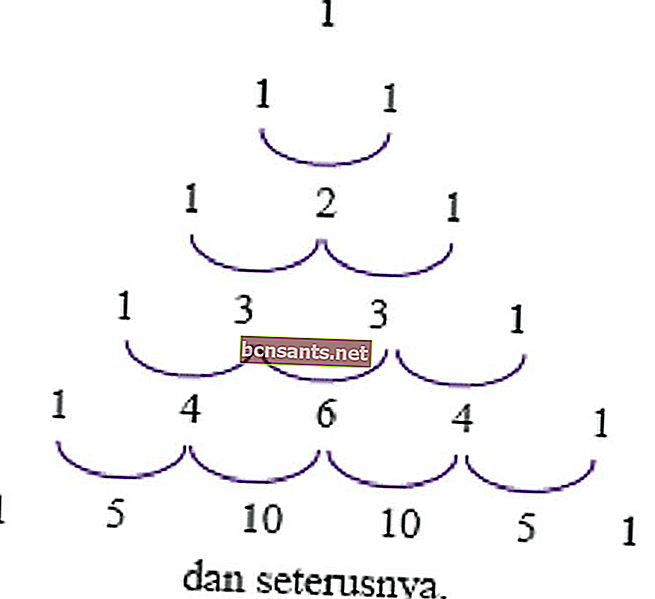
Bu üçgenin bir kullanımı, daha verimli hale getirmek için güç (a + b) veya (ab) katsayısını belirlemektir. Bu kullanım aşağıdaki örneklerde açıklanmaktadır.

Sorun örneği

İpucu: Pascal üçgenine dikkat edin.

1. (a + b) 4 çevirisi nedir?

Çözüm : (a + b) 4 için

• İlk olarak, a ve b değişkenleri, a4b veya a4'ten başlayarak düzenlenir.
• Sonra a'nın gücü 3'e düşer ki bu a3b1'dir (ab'nin toplam gücü 4 olmalıdır)
• Sonra 2'ye düşerek a2b2 olur
• Sonra 1'e düşer ve ab3 olur.
• Sonra a'nın gücü 0'a, b4'e düşer
• Daha sonra katsayılı denklemi boşluğun önüne yazın

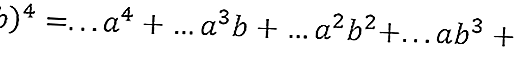
Şekil 2'ye göre 4. sırayla 1,4,6,4,1 sayıları elde edilerek (a + b) 4 öteleme elde edilir.

2. (a + b) 6'da a3b3 katsayısı nedir?

Ayrıca şunu okuyun: Manyetik Alan Malzemesi: Formüller, Örnek Problemler ve Açıklamalar

Çözüm :

Soru numarası 1'e göre, (a + b) 6'daki değişkenlerin sırası, yani

a6, a5b1, a4b2, a 3 b 3 .

Bu araçlar desen 1, 6, 15 dördüncü (Resim 2, sıra 6) içinde, bu 20 olan 20 . Böylece 20 a3b3 yazılabilir.

3. (3a + 2b) 3'ün çevirisini belirleyin

Yerleşme

Paskal üçgenin a ve b değişkenlerinin 3 üssüne toplamı olarak genel formülü aşağıdaki gibi sunulmuştur.

Değişkenleri 3a ve 2b olarak değiştirerek şunu elde ederiz