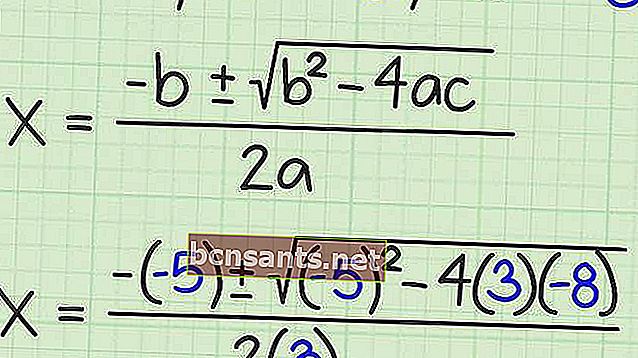
ABC formülü, sonuç bir tamsayı olmasa bile, çeşitli ikinci dereceden denklem biçimlerinin köklerini bulmanın mükemmel bir yoludur.
İkinci dereceden denklem ax2 + bx + c = 0, birkaç yöntem kullanılarak çözülebilir. Bunların arasında çarpanlara ayırma yöntemi, ABC karesini tamamlama ve formül vardır.
Bu yöntemler arasında abc formülü mükemmeldir çünkü sonuç bir tam sayı olmasa bile çeşitli ikinci dereceden denklem biçimlerinin köklerini bulmak için kullanılabilir.
Aşağıdaki, anlama, sorular ve tartışma dahil olmak üzere formülün daha ayrıntılı bir açıklamasıdır.
ABC formülünü anlamak
Abc formülü, ikinci dereceden bir denklemin köklerini bulmak için kullanılan formüllerden biridir. İşte bu formülün genel bir formu.

Abc formülündeki a, b ve c harflerine katsayı denir. X2'nin karesinin katsayısı a, x'in katsayısı b ve c sabitin katsayısıdır, genellikle sabit veya bağımsız bir terim olarak adlandırılır.
İkinci dereceden denklem temelde xy çeyreğindeki parabolün eğri geometrisini oluşturan matematiksel bir denklemdir.
Abc formülündeki katsayı değerinin aşağıdaki gibi birkaç anlamı vardır:
- a ikinci dereceden denklem tarafından oluşturulan içbükey / dışbükey prabolayı belirler. A> 0 değeri ise parabol yukarı doğru açılacaktır. Ancak, <0 ise parabol aşağı doğru açılacaktır.
- b, parabolün tepesinin x konumunu veya eğrinin ayna simetrisini belirler. Simetri ekseninin tam konumu ikinci dereceden denklemin -b / 2a'dır.
- c, y ekseninde veya x = 0 değeri olduğunda oluşan parabolik ikinci dereceden denklem fonksiyonunun kesişimini belirler.
Örnek Sorular ve Tartışma
İşte ikinci dereceden denklem problemlerinin bazı örnekleri ve bunların ikinci dereceden denklem formüllerini kullanarak çözümlerle tartışılması.
1. x2 + 7x + 10 = 0 ikinci dereceden denklemin köklerini abc formülünü kullanarak çözün !
Cevap:
Ayrıca şunu okuyun: Vücut İçin 7 Protein Fonksiyonu [Eksiksiz açıklama]a = 1, b = 7 ve c = 10 olduğuna dikkat edin
daha sonra denklemin kökleri:

Yani, x2 + 7x + 10 = 0 denkleminin köklerinin çarpımı x = -2 veya x = -5
2. abc formülünü kullanarak x2 + 2x = 0 için çözüm kümesini bulun
Cevap:
a = 1, b = 1, c = 0 olduğu için
Denklemin kökleri şu şekildedir:

Yani, x2 + 2x = 0 denkleminin köklerinin çarpımı x1 = 0 ve x2 = -2'dir, dolayısıyla çözüm kümesi HP = {-2,0}
3. x2 - 2x - 3 = 0 probleminde abc formülünü kullanarak x kök kümesini bulun.
Cevap:
a = 1, b = 2, c = -3 olduğu için
Denklemin köklerinin sonuçları aşağıdaki gibidir:

Dolayısıyla, x1 = -1 ve x2 = -3 ile çözüm kümesi HP = {-1,3}
4. x 2 + 12x + 32 = 0 ikinci dereceden denklemin sonucunu abc formülünü kullanarak belirleyin !
Cevap:
a = 1, b = 12 ve c = 32 olduğuna dikkat edin
Denklemin kökleri şu şekildedir:

Öyleyse, ikinci dereceden denklem için köklerin sonuçları -4 ve -8'dir.
5. Aşağıdaki problemden seti bulun 3x2 - x - 2 = 0
Cevap:
a = 3, b = -1, c = -2 olduğuna dikkat edin
Denklemin kökleri şu şekildedir:

Dolayısıyla, ikinci dereceden denklem 3x2 - x - 2 = 0'ın kökleri x1 = 1 ve x2 = -2 / 3'tür, dolayısıyla çözüm kümesi HP = {1, -2 / 3}
6. x 2 + 8x + 12 = 0 denkleminin köklerini abc formülünü kullanarak bulun !
Cevap:
a = 1, b = 8 ve c = 12 olduğuna dikkat edin
daha sonra ikinci dereceden denklemin kökleri aşağıdaki gibidir:

Dolayısıyla, ikinci dereceden denklem x2 + 8x + 12 = 0'ın kökleri x1 = -6 veya x2 = -2'dir, böylece çözüm kümesi HP = {-6, -2} olur
7. x 2 - 6x - 7 = 0 denkleminin köklerini abc formülüyle çözün .
Cevap:
a = 1, b = - 6 ve c = - 7 olduğu bilinmektedir
Denklemin kökleri şu şekildedir:
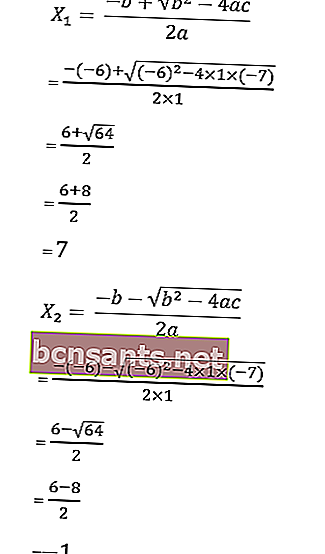
Yani kökler x 1 = 1 veya x 2 = 5/2, dolayısıyla çözüm kümesi HP = {1, 5/2}.
Ayrıca şunu okuyun: İkinci Dereceden Denklemler (TAM): Tanım, Formüller, Örnek Problemler8. 2x 2 - 7x + 5 = 0 denkleminin köklerini abc formülüyle bulun
Cevap:
a = 2, b = - 7 ve c = 5 olduğu için
Denklemin kökleri şu şekildedir:
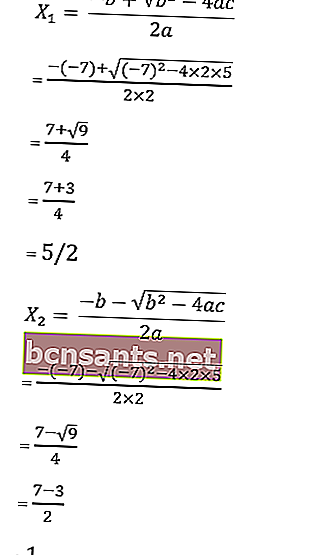
Yani kökler x1 = –4 veya x2 = 5/3, dolayısıyla çözüm kümesi HP = {1, 5/3}.
9. 3x 2 + 7x - 20 = 0 denklemini abc formülüyle çözün .
Cevap:
a = 3, b = 7 ve c = - 20 olduğuna dikkat edin
sonra denklemin kökleri:
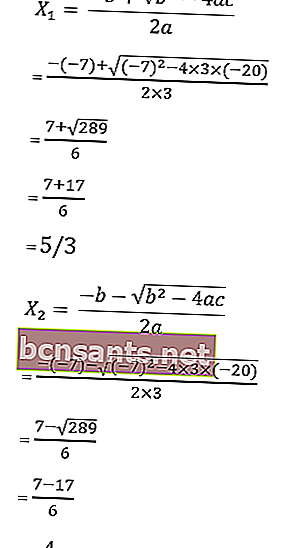
Yani kökler x1 = –4 veya x2 = 5/3, dolayısıyla çözüm kümesi HP = {-4, 5/3}.
10. 2x 2 + 3x +5 = 0 denkleminin köklerini abc formülüyle bulun .
Cevap:
a = 2, b = 3 ve c = 5 olduğunu biliyoruz
Denklemin kökleri şu şekildedir:
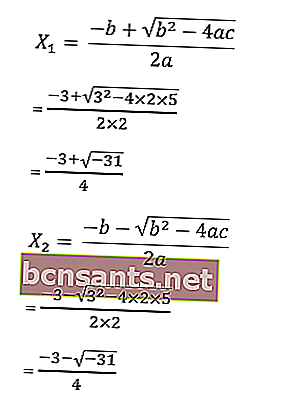
2x2 + 3x +5 = 0 denkleminin kökünün sonucu √ - 31 hayali kök numarasına sahiptir, dolayısıyla denklemin çözümü yoktur. Çözüm kümesi, HP = {∅} boş küme olarak yazılır.
Bu, soru örnekleri ve tartışmaları ile abc formülünün tanımının bir açıklamasıdır. Faydalı olabilir!
