
Bir üçgenin şeklinin alanını bulmak için formül 1/2 x taban x yüksekliktir, üçgenin her iki kenarının uzunluklarını ekleyerek bulunabileceği üçgenin çevresini bulmak için.
Matematikte bize çeşitli şekiller öğretilir. Bunlardan biri üçgen şeklidir. Üçgenin şekli, çeşitli şekil türleri arasında en basit şekildir.
Bir üçgen, bir parça ile sınırlanmış üç açıya sahip üç kenardan oluşur. Ayrıca üçgenin toplam açısı 180 derecedir.
Birkaç çeşit üçgen vardır. Kenarların uzunluğuna bağlı olarak, eşit kenar uzunluklarına sahip eşkenar üçgenler, bacakların iki eşit kenarı olan ikizkenar üçgenler ve üç kenarın farklı uzunluklarına sahip herhangi bir üçgen vardır.
Bu arada, açıya göre, 90 dereceden küçük bir açıya sahip bir dar üçgen, 90 dereceden fazla bir açıya sahip geniş bir üçgen ve 90 derecelik bir açılı bir dik üçgen vardır.
Üçgenlerle ilgili olarak, üçgenin alanı ve çevresi dahil bilinmesi gereken birkaç bileşen vardır. Aşağıda, sorunun bir örneği ile birlikte üçgenin alanı ve çevresinin bir açıklaması yer almaktadır.
Üçgenin Alanı

Alan, alan veya alan, iki boyutlu boyutu ifade eden bir miktardır, yani kapalı bir eğri veya çizgi ile açıkça tanımlanan yüzeyin bir kısmı.
Üçgenin alanı, üçgenin kendisinin boyutudur. Bir üçgenin alanı için formül şu şekildedir:
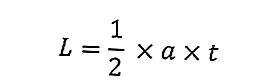
burada L üçgenin alanıdır (cm 2 ), a üçgenin tabanıdır (cm) ve h üçgenin yüksekliğidir (cm).
Üçgen Probleminin Alan Örneği
Örnek Problem 1
Taban uzunluğu a = 10 cm ve yüksekliği h = 8 cm olan bir dar üçgen vardır. Üçgenin alanını hesaplayın.
Ayrıca şunu okuyun: Hayvanlar: Özellikler, Türler, Örnekler [TAM açıklama]Çözüm:
Eğer: a = 10 cm, h = 8 cm
Aranıyor: Üçgenin alanı?
Cevap:
L = ½ xaxt
= ½ x 10 x 8
= 40 cm2
Yani, akut üçgenin alanı 40 cm2'dir.
Örnek Problem 2
Dik üçgenin tabanı 15 cm ve yüksekliği 20 cm'dir. Dik üçgenin alanını bulun ve hesaplayın.
Çözüm:
Eğer: a = 15 cm, h = 20 cm
Aranıyor: Üçgenin alanı?
Cevap:
L = ½ xaxt
= ½ x 15 x 20
= 150 cm2
Yani, dik üçgenin alanı 150 cm2
Örnek Problem 3
Tabanı 8 cm ve yüksekliği 3 cm olan geniş bir üçgen, o zaman üçgenin alanı nedir?
Çözüm:
Biliyorsunuz: a = 8 cm, h = 3 cm
Aranıyor: Üçgenin alanı?
Cevap:
L = ½ xaxt
= ½ x 8 x 3
= 12 cm2
Yani, geniş üçgenin alanı 12 cm2'dir.
Örnek Problem 4
Aynı kenar uzunluğuna sahip bir ikizkenar üçgen 13 cm ve üçgenin tabanı 10 cm'dir. İkizkenar üçgenin alanı nedir?
Çözüm:
Bilirsiniz: s = 13 cm, a = 10 cm
Aranıyor: Üçgenin alanı?
Cevap:
Üçgenin yüksekliği bilinmediğinden, üçgenin yüksekliğini bulmak için Pisagor formülünü kullanıyoruz:

Üçgenin yüksekliği bilindiğinden, o zaman:
L = ½ xaxt
= ½ x 10 x 12
= 60 cm2
Yani ikizkenar üçgenin alanı 60 cm2
Üçgenin Çevresi

Çevre, iki boyutlu bir şeklin kenarlarının sayısıdır. Öyleyse, üçgenin çevresi, üçgenin kendisinin kenarlarının toplamıdır.
İşte bir üçgenin çevresi için formül:
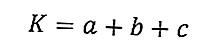
K, üçgenin çevresi (cm) ve a, b, c, üçgenin (cm) yan uzunluklarıdır.
Bir üçgenin çevresi örneği
Örnek Problem 1
Bir eşkenar üçgenin 15 cm uzunluğunda kenarları vardır. Üçgenin çevresi nedir?
Çözüm:
Bilirsiniz: yan uzunluk = 15 cm
Sorulan: çevre =….?
Cevap:
K = taraf a + taraf b + c tarafı
eşkenar üçgen olduğu için üç kenarın uzunlukları eşittir.
K = 15 + 15 + 15
= 45 cm
Yani , eşkenar üçgenin çevresi 45 cm
Ayrıca şunu okuyun: Sosyal Etkileşim - Tam Tanım ve AçıklamaÖrnek Problem 2
Rasgele bir üçgenin kenarları 3 cm, 5 cm ve 8 cm'dir. Üçgenin çevresini hesaplayın.
Çözüm:
Bilirsiniz: a = 3 cm, b = 5 cm ve c = 8 cm
Sorulan: çevre =….?
Cevap:
K = taraf a + taraf b + c tarafı
= 3 + 5 + 8
= 16 cm
Yani üçgenin çevresi 16 cm
Örnek Problem 3
Bir ikizkenar üçgenin kenarları 10 cm'ye eşit ve tabanı 6 cm'dir. İkizkenar üçgenin çevresini hesaplayın.
Çözüm:
Kenarların 10 cm, 6 cm uzunluğunda olduğunu biliyorsunuz
Sorulan: çevre =….?
Cevap:
K = taraf a + taraf b + c tarafı
üçgen ikizkenar olduğundan, aynı uzunlukta iki kenar vardır, yani 10 cm, sonra K = 10 + 10 + 6 = 26 cm
Yani ikizkenar üçgenin çevresi 26 cm
Örnek Problem 4
Bir ikizkenar üçgenin yüksekliği 8 cm ve tabanı 12 cm'dir. Üçgenin çevresini hesaplayın.
Çözüm:
Bilirsiniz: üçgenin yüksekliği h = 8 cm
tabanın yanı a = 12 cm
Sorulan : çevre =….?
Cevap:
K = taraf a + taraf b + c tarafı
Üçgenin iki kenarı bilinmiyor, bu yüzden o kenarın uzunluğunu bulmak için Pisagor formülünü kullanıyoruz.

K = 10 + 10 + 12
K = 32 cm
Yani ikizkenar üçgenin çevresi 32 cm
Bu, bir üçgenin alanının ve üçgenin çevresinin, örnekler ve tartışmalarla birlikte açıklamasıdır. Faydalı olabilir.
