
Aritmetik seriler, matematikte çeşitli şekillerde çok önemli faydaları olan bir seri numarası örüntüsüdür.
Örneğin, tasarruf ettiğinizde, her gün düzenli olarak beş bin rupi harçlık bırakırsınız, ertesi gün bu on bin rupi olacaktır vb. Zamanla paranız artar, değil mi?
Bu toplama modeline aritmetik seri denir.
Aritmetik dizileri tartışmadan önce, aritmetik dizileri anlamalıyız çünkü aritmetik dizilerle elde edilen toplama kalıpları aritmetik dizilerden gelir.
Aritmetik Diziler
Aritmetik dizi (Un), toplama ve çıkarma işlemlerine dayanan sabit bir modele sahip bir sayı dizisidir.
Aritmetik sıra, birinci terim (U 1 ), ikinci terim (U 2 ) ve nci terim (Un) kadar çoktan oluşur.
Her kabilenin aynı farkı veya farkı vardır. Her kabile arasındaki fark, b olarak sembolize edilen farklılık denen şeydir . İlk U 1 terimi de a olarak sembolize edilir .
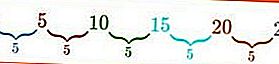
Aritmetik dizi: 0,5,10,15,20,25,…., Un
Örneğin yukarıdaki, aynı farka sahip olan bir aritmetik dizidir, yani b = 5 ve ilk terim a = 0'dır. Fark, her kabilenin çıkarılmasıyla elde edilir. Örneğin ikinci terim U 2 eksi birinci terim U 1 , b = U 2 - U 1 = 5 - 0 = 5, b'nin değeri de üçüncü terim eksi ikinci terimden elde edilebilir ve benzeri, kolay değil mi?
Şimdi, n'inci terimin (Un) formülünü bulmak için kullanımı kolay pratik bir formül kullanabiliriz.

Burada, Un n'inci terimdir, u , n-1 , n önce bir terimdir, bir ilk dönem , b farkı ve n, bir tam sayı olduğu.
Aritmetik seri materyali hakkında daha fazla ayrıntı için aşağıdaki örnek soruları göz önünde bulundurun,
1. Bir aritmetik dizi verildiğinde 3,7,11,15,…., Un. Yukarıdaki onuncu terim U 10 satırı nedir?
Ayrıca şunu okuyun: Tüm Zamanların 25'ten Fazla Önerilen En İyi Bilim Filmi [En Son GÜNCELLEME]Tartışma:
İlk dönem, yukarıda bu diziden bilinen bir 3'tür, bir fark vardır , b, yani 4 ve n = 10.
U 10'un onuncu terimi nedir ? önceki formül kullanılarak U 10 aşağıdaki gibi elde edilir
U n = a + (n-1) b
U 10 = 3 + (10-1) 4
= 3 + 36
= 39
Dolayısıyla, yukarıdaki aritmetik dizideki onuncu terim 39'dur.
Aritmetik ilerleme
Daha önce tartışıldığı gibi, Aritmetik dizi , aynı modele sahip U 1 , U 2 , ..., U n sayılarının dizisini belirtir . Bu arada, aritmetik sıra, U 1 + U 2 +… + Un aritmetik dizisindeki sayı düzenlemesinin n- terimine toplamıdır .
Bu aritmetik serinin asıl kavramı basittir, çünkü yalnızca daha önce tartıştığımız aritmetik diziyi n'inci terime, neyin sıralandığına bağlı olarak ekleriz.
Örneğin, önceki örnek problem dizisini dördüncü terime ekliyoruz, kolay değil mi? Peki ya aritmetik diziyi 100. terime eklerseniz, nasıl oluyor da bu kadar zor oluyor?
Bu nedenle, bu aritmetik seriyi hesaplamayı kolaylaştırmak için pratik bir formül kullanılır.
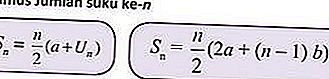
İle,
a ilk terim
b farklı
Sn, n'inci terimin sayısıdır
Aritmetik seri problemlerine örnek
Aritmetik bir dizi verildiğinde 3 + 7 + 11 + 15 +…. + Un. Yukarıdaki serideki onuncu terim U 10'un numarasını belirleyin
Tartışma :
A = 3, b = 4 ve n = 10'un üzerindeki serilerde yukarıdaki serideki 10. terim sayısının kaç olduğu sorulduğu bilinmektedir.
Bir formül kullanarak
Sn = n / 2 (2a + (n-1) b)
S 10 = 10/2 (2.3+ (10-1). 4)
= 5. (6 + 36)
= 210
Yani, yukarıdaki on terim dizisinin sayısı 252
Dolayısıyla, aritmetik serilerle ilgili malzemeyi zaten anladınız, seri problemlerle çalışma konusunda daha da yetkin olmak için aşağıdaki örnek soruları düşünün.
1. İlk 10 terim ve altıncı terim 20 ile aritmetik bir dizi vardır.
a. Aritmetik serideki farkı belirleyin.
b. Aritmetik sırayı yazın.
c. Aritmetik dizinin ilk altı teriminin toplamını belirleyin.
Ayrıca şunu okuyun: Ana fikir / ana fikir ... (Tanım, türler ve özellikler) TAMAMLANDITartışma :
A = 10 ve U6 = 20 ise,
a. Un = a + (n-1) b
U6 = a + (6-1) b
20 = 10+ (5) b
b = 10/5 = 2
b. Aritmetik sıra: 10 + 12 + 14 + 16 + 18 + 20 +… + Un
c. Altıncı dönem S6,
Sn = n / 2 (2a + (n-1) b)
S6 = 6/2 (2,10+ (6-1) 2)
= 3 (20 + 10)
= 90
Yani, yukarıdaki serideki altıncı terimin toplamı 90'dır.
2. Bir aritmetik sıra verildiğinde: 2, 6, 10, 14, 18, ……… U n . Aritmetik dizideki n'inci terimin formülünü belirleyin.
Tartışma:
Yukarıdaki aritmetik çizginin, a = 2 ve b = 4 olduğu varsayılırsa, n'inci terim için formül istenir
Un = a + (n-1) b
Un = 2+ (n-1) 4
Un = 2 + 4n-4
Un = 4n-2
Dolayısıyla, yukarıdaki satırın n'inci formülü Un = 4n-2'dir.
Aritmetik serilerle ilgili malzeme budur, umarım onu iyi anlayabilirsiniz!
Referans : Aritmetik Dizi ve Toplam - Matematik Eğlencelidir
