
Çevre formülü K = 2 × π × r şeklindedir, burada K = çemberin çevresi, π = sabit pi (3.14) ve r = çemberin yarıçapı. Aşağıda, örnek bir problemle birlikte daha eksiksiz bir açıklama yer almaktadır.
Tekerleğin icadı, dairesel şekillerin günlük yaşamdaki önemi hakkındaki temel keşiflerden biridir.
Sadece tekerlekler değil, araba lastikleri, madeni paralar, duvar saatleri, lolipoplar, DVD bantları, şişe kapakları, holahoplar ve diğerleri gibi etrafa bakarsak hala birçok dairesel uygulama var.

Tamam, bu daire şekli çok önemli değil mi? Açıkçası çok önemli. Öyleyse, çember ve çember formülleri hakkında daha fazla bilgi edinelim.
Bir Çevre Oluşturun
Bir daire, dairenin merkezinde aynı uzunlukta eğriler / eğriler oluşturan bir dizi noktadan oluşan iki boyutlu bir şekildir. Burada P noktası çemberin merkezidir.
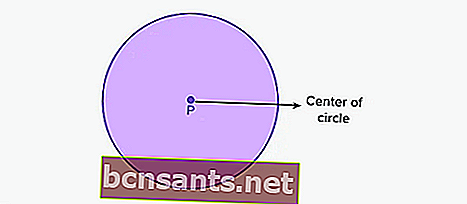
Çemberin merkezinden tüm noktalarda aynı uzunluk veya mesafeye çemberin yarıçapı denir . Bu arada, bir çemberin dış noktalarını birleştiren en uzun mesafeye çemberin çapı denir .
Yarıçap ve çapın yanı sıra, bir dairenin daire, dairesel yay, iskelet ve akor gibi başka unsurları da vardır.
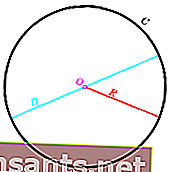
Dairenin ayrıca alanı ve çevresi vardır. Bir sonraki tartışmada, örnek bir problemle birlikte tam bir çemberin çevresi için formül tartışmaya odaklanacağız.
Bir çemberin çevresi için formül
Bir çemberin çevresi , orijinal noktaya dönmek için çemberin üzerindeki bir noktadan bir turdaki mesafedir. ya da dairenin uzunluğunun bir ölçüsü olarak da yorumlanabilir.
Bir deneyimiz olduğunu varsayalım, dairesel şekilli üç farklı nesne var. Sonra nesnenin çemberinin çevresini ve çapını ölçüyoruz. Aşağıdaki tabloda gösterildiği gibi:
Örneğin, metal bir bileziğimiz varsa. Daha sonra bilezik düz bir metal çubuk oluşturmak için kesilir, ardından metal çubuğun uzunluğu bileziğin çevresi veya dairenin çevresidir.
| Şey | Çevre (K) | Çap (d) | C / d = π |
| Maden suyu kutusu | 24 santimetre | 7,7 cm | 3.11 |
| Süt kutuları | 21,5 cm | 7.0 cm | 3.07 |
| Plastik saklama kabı | 35,5 cm | 11 santimetre | 3.22 |
Bundan sonra, çevrenin çapa oranını hesaplıyoruz ve nesnenin üç K / d oranının ortalaması (3.11+ 3.07 +3.22) / 3 = 3.13.
Evet, K / d oranı her zaman 3,14 veya 22 / 7'ye yakındır. Bu, bir çemberin çevresinin çapa oranının sabit olduğu veya genellikle π (okuma: phi) ile ifade edildiği anlamına gelir.
Yani, π = C / d = 3.14 veya 22/7 değeri
Her iki taraf da d ile çarpılırsa, şunu elde ederiz,
C = π d
Bilgi:
K = çemberin çevresi
d = daire çapı
π = 3.14 veya 22/7
Çap 2x'e eşit olduğundan, çemberin yarıçapı d = 2r, çemberin çevresi,
C = πd = π.2r
C = 2 π r
Bilgi:
K = çemberin çevresi
r = dairenin yarıçapı
π = 3.14 veya 22/7
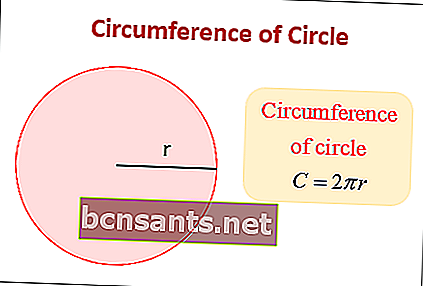
Çevre Formülü ile Örnek Problem
1. Bir dairenin çevresi 396 cm'dir. Çemberin yarıçapını hesaplayın!
Bilinen:
- K = 396 cm
Diye sordu:
- r dairenin yarıçapı?
Cevap:
C = 2 π r
396 = 2 π r
396,7 = 2. 22/7. r
r = 2772/44
r = 63 cm
Daha sonra dairenin yarıçapı 63 cm'dir.
2. 14 cm yarıçaplı bir çemberin çevresini π = 22/7 ile bulun
Bilinen:
- r = 14 cm
- π = 22/7
Diye sordu:
- Çemberin çevresi nedir?
Cevap:
C = 2 π r
K = 2 x 22/7 x 14
K = 2 x 22 x 2
K = 88 cm
Yani dairenin çevresi 88 cm
3. π = 3.14 ile 10 cm çapında bir çemberin çevresini bulun.
Bilinen:
- d = 10 cm
- π = 3.14
Diye sordu:
Çemberin çevresi nedir?
Cevap:
C = π d
K = 3,14 x 10
K = 31,4 cm
Yani dairenin çevresi 31,4 cm
4. Aşağıdaki gölgeli alanın çevresini hesaplayın!
Bilinen:
- r = 14 cm
Diye sordu:
Gölgeli alanın etrafında mı?
Cevap:
Çevrenin üstündeki görüntü, bir karenin çevresi artı çemberin yarısından oluşur ve karenin aynı çapına ve kenarına sahip bir yarım daire ile çıkarılır, ardından çevre formülü olur
Ayrıca şunu okuyun: İletkenler - Açıklamalar, Çizimler ve ÖrneklerÇevre = 14 + 14 + ½ K + ½ K
= 14 + 14 + ½ π d + ½ π d
= 14 + 14 + ½. 22/7. 14 + ½. 22/7. 14
= 28 + 22+ 22
Çevre = 72 cm
Yani gölgeli alanın çevresi 72 cm'ye eşittir.
5. Budi, 84 cm çapında tekerlekleri olan ve 1000 kez dönen bir motosiklete sahiptir, arabanın ne kadar yol katettiğini hesaplayınız?
Bilinen:
- d = 84 cm
- n = 1000 kez
Diye sordu:
Motosiklet ne kadar uzağa gidiyor?
Cevap:
Motorun çemberin çevresinin 1000 katı kadar kat ettiği mesafe = n / 2 = 1000/2 = 500
Daha sonra motorun kat ettiği mesafe = 500x π d = 500.3,14. 84 = 131,880 cm = 1,31 km
6. Çapı 40 cm ise dairenin çevresi nedir?
Cevap:
- Çevre = π xd
- = 3,14 x 40
- = 125,66
Yani dairenin çevresi 125.66 cm'dir.
7. Çapı 20 cm olan dairenin çevresini hesaplayın.
Yerleşme:
Bilinen:
- d = 20 cm
- π = 3.14
Sorulan: Çemberin etrafında mı?
Cevap:
- Çevre = π × d
- Çevre = 3.14 × 20
- Çevre = 62,8 cm
Yani dairenin çevresi 62,8 cm'dir.
Bu, bir çemberin çevresi için tam formüllerin eksiksiz bir açıklaması ve örnek bir problemdir. Faydalı olabilir!
Referans:
- Çemberin Çevreleri - Khan Academy
- Çemberin Çevresi Nasıl Hesaplanır - Wikihow
