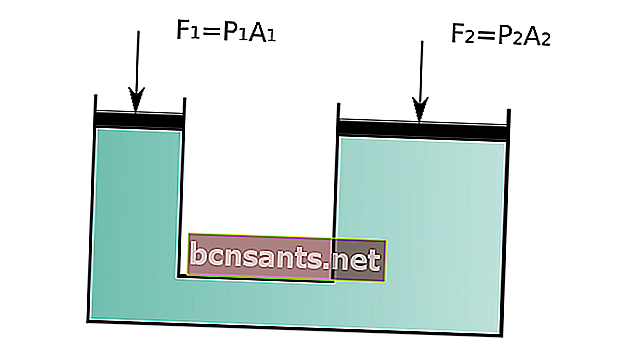
Pascal yasası şöyle der: "Kapalı bir sisteme harici basınç uygulanırsa, sıvının herhangi bir noktasındaki basınç, uygulanan harici basınca orantılı olarak artacaktır."
Bir tamir atölyesinin lastik değiştirdiğini gördünüz mü? Eğer öyleyse, kesinlikle önce kriko adı verilen küçük bir aletle arabanın veya hatta kamyonun kaldırıldığını göreceksiniz.
Elbette soru, bir krikonun binlerce kez ağırlığındaki bir arabayı krikodan nasıl kaldırabildiğidir.

Bu sorunun cevabı Pascal Yasası adlı bir yasa ile açıklanmaktadır. Daha fazla ayrıntı için, problemin bir örneğiyle birlikte Pascal Yasasına daha fazla bakalım.
Pascal Yasasını Anlamak
16. yüzyılda, Blaise Pascal adlı bir filozof ve bilim adamı, Pascal Yasası adlı bir yasa icat etti. Bu yasa okur:
"Kapalı bir sisteme harici basınç uygulanırsa, sıvının herhangi bir noktasındaki basınç, harici olarak uygulanan basınçla orantılı olarak artacaktır."
Bu kanunun temel bilimi, sıvıya kapalı sistemle uygulanan basıncın, sistemden çıkan basınca eşit olacağı basınçtır.
Onun sayesinde, özellikle ağır bir yükü kaldırma sorununu çözmek için yenilikler ortaya çıkmaya başladı. Örnekler, frenlemede krikolar, pompalar ve hidrolik sistemlerdir.
Formül
Pascal Yasasının denklemlerine veya formüllerine geçmeden önce, temel bilimi, yani basıncı öğrenmemiz gerekir. Basıncın genel tanımı, bir yüzeye etki eden bir kuvvetin etkisi veya etkisidir. Denklemin genel formülü:
P = F / A
Nerede :
P basınçtır (Pa)
F kuvvettir (N)
A, etkili yüzey alanıdır (m2)
Pascal Yasasının matematiksel denklemi şu durumlarda çok basittir:
Ayrıca şunu okuyun: Bakteriyel yapı, işlevler ve resimler [TAM]Enter = Çıkış
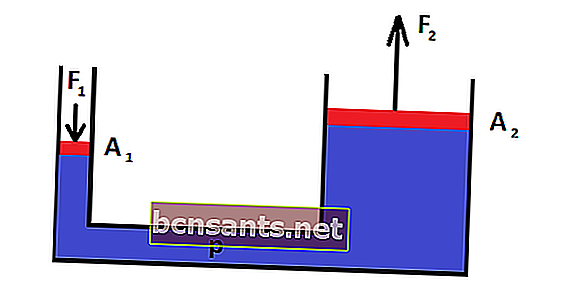
Yukarıdaki resim ile Pascal Yasasının denklemi şu şekilde yazılabilir:
P1 = P2
F1 / A1 = F2 / A2
İle:
P1: giriş basıncı (Pa)
P2: çıkış basıncı (Pa)
F1: uygulanan kuvvet (N)
F2: üretilen kuvvet (N)
A1: uygulanan kuvvet alanı (m2)
A2: elde edilen alan (m2)
Ek olarak, Pascal Yasasını uygularken kullanılan ve mekanik avantaj olarak adlandırılan başka bir terim vardır. Genel olarak mekanik avantaj, bir sistemin üretebileceği kuvvet ile uygulanması gereken kuvvet arasındaki orandır. Matematiksel olarak mekanik avantaj şöyle yazılabilir:
mekanik avantaj = F2 / F1
Hidrolik araba asansörü örneğinde olduğu gibi, sistemdeki sıvı her zaman aynı hacme sahip olacaktır.

Bu nedenle, Pascal Yasasının denklemi, aynı zamanda, içeri ve dışarı hacim oranı olarak da yazılabilir.
V1 = V2
veya şu şekilde yazılabilir
A1.h1 = A2.h2
Nerede :
V1 = içeri itilen hacim
V2 = çıkan hacim
A1 = giriş bölümü alanı
A2 = kesit alanından çık
h1 = gelen bölümün derinliği
h2 = çıkış bölümünün yüksekliği
Sorun örneği
Aşağıda, daha kolay anlayabilmeniz için Pascal Yasasının uygulanmasıyla ilgili bazı örnekler ve sorunların tartışılması bulunmaktadır.
örnek 1
1 tonluk bir yükü kaldırmak için bir hidrolik kaldıraç kullanılır. Kesit alanları arasındaki oran 1: 200 ise, hidrolik kola uygulanması gereken minimum kuvvet nedir?
Cevap:
A1 / A2 = 1: 200
m = 1000 kg, sonra W = m. g = 1000. 10 = 10000 N
F1 / A1 = F2 / A2
F1 / F2 = A1 / A2
F1 / 10000 = 1/200
F1 = 50N
Yani sistemin yapması gereken kuvvet 50N
Örnek 2
Hidrolik kolun mekanik avantajı 20 değerindedir. Bir kişi 879 kg ağırlığındaki bir aracı kaldırmak isterse, sistemin ne gibi bir kuvvet yapması gerekir?
Cevap:
m = 879kg, sonra W = mg = 879. 10 = 8790 N
mekanik kazanç = 20
F2 / F1 = 20
8790 / F1 = 20
F1 = 439,5 N
yani kaldıraç üzerine uygulanan kuvvet 439,5 N
Ayrıca şunu okuyun: 1 Yıl Kaç Hafta? (Yıllardan Haftaya) İşte CevapÖrnek 3
Hidrolik bir kolun giriş pistonu çapı 14 cm ve çıkış çapı 42 cm'dir. Piston 10 cm derinliğe inerse, çıkarılan pistonun yüksekliği nedir?
Cevap:
Piston, dairesel bir yüzeye sahiptir, bu nedenle alanı
A1 = π. r12 = 22/7. (14/2) 2 = 154 cm2
A2 = π. r22 = 22/7. (42/2) 2 = 1386 cm2
h1 = 10 cm
sonra
A1. h1 = A2. h2
154. 10 = 1386. h2
h2 = 1540/1386
h2 = 1,11 cm
Yani dışarı çıkan piston 1.11 cm yüksekliğinde
Örnek 4
Musluğa bağlı bir hortumu olan bir kompresörün çapı 14 mm'dir. Hortumun ucuna 0,42 mm ağızlı bir püskürtücü takılırsa ve kompresör çalıştırıldığında, basınç 10 bar olarak ölçülür. Kompresör basıncının düşmemesi durumunda nozuldan çıkan hava egzoz kuvveti miktarını belirleyin.
Cevap :
Hortumlar ve delikler dairesel bir kesit alanına sahiptir
Daha sonra delik yüzeyinin alanı
A2 = π. r22 = 22/7. (1,4 / 2) 2 = 1,54 mm2
"Unutmayın ki, Pascal Yasası içerideki basıncın dışarıdaki basınca eşit olduğunu açıklar."
Böylece ortaya çıkan hava kuvveti:
P = F / A
F = P. Bir
F = 10 bar. 1.54 mm2
birim çubuğunu paskal ve mm2'yi m2 olarak değiştirin
sonra
F = 106 Pa. 1,54 x 10-6 m2
F = 1.54 N
Yani ortaya çıkan rüzgar kuvveti 1.54 N
Bu nedenle, Pascal Yasası hakkındaki tartışma, umarım sizin için yararlı olabilir.
