
Bileşim işlevi , yeni bir işlev üretebilmesi için iki tür f (x) ve g (x) işlevinin bir işleminin birleşimidir.
Kompozisyon Fonksiyon Formülleri
Kompozisyon işlevi işleminin sembolü "o" ile olduğundan kompozisyon veya daire okunabilir. Bu yeni fonksiyon f (x) ve g (x) 'den oluşturulabilir, yani:
- (sis) (x) bu, g'nin f'ye girildiği anlamına gelir
- (gof) (x) f'nin g'ye konulduğu anlamına gelir
Kompozisyonda işlev, tek bir işlev olarak da bilinir.
Tek işlev nedir?
Tek bir işlev, "sis" harfiyle gösterilebilen veya "f döner kavşak g" olarak okunabilen bir işlevdir. "Sis" işlevi g'nin önce yapılan ve ardından f tarafından takip edilen işlevidir.
Bu arada, "gof" işlevi g roundabout f işlevini okur. Dolayısıyla, "gof", f'nin g yerine önce yapıldığı bir fonksiyondur.
Daha sonra (sis) (x) = f (g (x)) → fonksiyon g (x) f (x) fonksiyonu olarak oluşur.
Bu işlevi anlamak için aşağıdaki resme bakın:
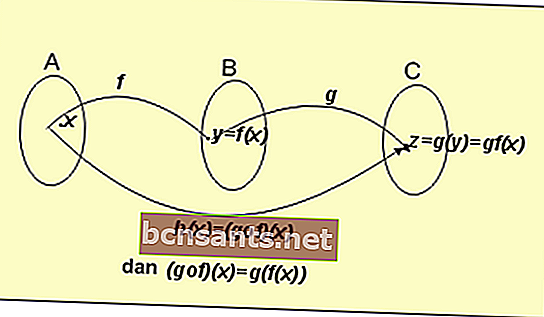
Yukarıdaki formül şemasından elde ettiğimiz tanım şudur:
Eğer f: A → B, y = f (x) formülüyle belirlenir.
Eğer g: B → C, y = g (x) formülüyle belirlenir.
Sonra, g ve f fonksiyonlarının bir sonucunu elde ederiz:
h (x) = (gof) (x) = g (f (x))
Yukarıdaki tanımdan f ve g fonksiyonlarını içeren fonksiyonların yazılabileceği sonucuna varabiliriz:
- (gof) (x) = g (f (x))
- (sis) (x) = f (g (x))
Kompozisyon Fonksiyonunun Özellikleri
Aşağıda açıklanan kompozisyon işlevinin birkaç özelliği vardır.
Eğer f: A → B, g: B → C, h: C → D ise, o zaman:
- (sis) (x) ≠ (gof) (x). Değişmeli doğa geçerli değil
- [fo (goh) (x)] = [(sis) oh (x)]. ilişkiseldir
- Özdeşlik işlevi I (x) ise, (fol) (x) = (lof) (x) = f (x)
Sorun örneği
Problem 1
Sırasıyla f (x) ve g (x) olmak üzere iki işlev verildiğinde :
f (x) = 3x + 2
g (x) = 2 - x
Belirleyin:
a) ( f o g ) (x)
b) ( g o f ) (x)
Cevap
Bilinen:
f (x) = 3x + 2
g (x) = 2 - x
( f o g ) (x)
" G (x) 'i f (x) içine yerleştirin "
olmak:
( f o g ) (x) = f ( g (x))
= f (2 - x)
= 3 (2 - x) + 2
= 6 - 3x + 2
= - 3x + 8
( g o f ) (x)
" F (x) 'i g (x)' e yerleştirin"
Olana kadar:
( f o g ) (x) = g ( f (x))
= g (3x + 2)
= 2 - (3x + 2)
= 2 - 3x - 2
= - 3x
Problem 2
F (x) = 3x + 4 ve g (x) = 3x olduğu biliniyorsa (sis) (2) 'nin değeri nedir.
Cevap:
(sis) (x) = f (g (x))
= 3 (3x) + 4
= 9x + 4
(sis) (2) = 9 (2) + 4
= 22
Sorun 3
Fonksiyonu göz önüne alındığında , f (x) = 3x - 1 ve g fonksiyonunun bileşimin (x) = 2 x 2 + 3 değeri ( g O f ) (1) = ....?
Cevap
Bilinen:
f (x) = 3x - 1 ve g (x) = 2 × 2 + 3
( g o f ) (1) =…?
F (x) 'i g (x)' e yerleştirin ve ardından 1 ile doldurun
( g o f ) (x) = 2 (3 x - 1) 2 + 3
( g o f ) (x) = 2 (9 x 2 - 6x + 1) + 3
( g o f ) (x) = 18x 2 - 12x + 2 + 3
( g o f ) (x) = 18 × 2 - 12x + 5
( g o f ) (1) = 18 (1) 2-12 (1) + 5 = 11
Sorun 4
İki işlevi vardır:
f (x) = 2x - 3
g (x) = x2 + 2x + 3
Eğer (sis) (a) 33 ise, 5a'nın değerini bulun
Cevap:
Önce ara (sis) (x)
(sis) (x) eşittir 2 (x2 + 2x + 3) - 3
(sis) (x) eşittir 2 × 2 4x + 6 - 3
(sis) (x) 2 × 2 4x + 3'e eşittir
33, 2a2 4a + 3 ile aynıdır
2a2 4a - 30 eşittir 0
a2 + 2a - 15 eşittir 0
Ayrıca şunu okuyun: İş Formülleri: Materyal Açıklaması, Soru Örnekleri ve TartışmaFaktör:
(a + 5) (a - 3) eşittir 0
a = - 5 veya a eşittir 3
İçin
5a = 5 (−5) = −25 veya 5a = 5 (3) = 15
Sorun 5
Eğer (sis) (x) = x² + 3x + 4 ve g (x) = 4x - 5. f (3) 'ün değeri nedir?
Cevap:
(sis) (x) eşittir x² + 3x + 4
f (g (x)) eşittir x² + 3x + 4
g (x) eşittir 3 Yani,
4x - 5 eşittir 3
4x eşittir 8
x 2'ye eşittir
f (g (x)) = x² + 3x + 4 ve g (x) eşittir 3 için x eşittir 2
Kadar: f (3) = 2² + 3. 2 + 4 = 4 + 6 + 4 = 14
Bu nedenle, Bileşim Fonksiyonu formülüne ilişkin açıklama, sorunun bir örneğidir. Faydalı olabilir.
