Sin Cos Tan Trigonometrik Tabloyu (Tüm Açıları) Tamamlayın + Nasıl Anlaşılır

Trigonometrik tablo sin cos tan, bir açının trigonometrik değerini veya sin cos tanjantını içeren bir dizi tablodur.

Bu makalede, günah cos tan için trigonometrik değerler tablosu 0º ila 360º açılardan (veya genellikle 360 derecelik daire açısı olarak adlandırılan) çeşitli özel açılardan gösterilmektedir, böylece artık bunları ezberlemek zorunda kalmazsınız.

Trigonometrik özdeşlik formülüne gelince, bunu bu makalede okuyabilirsiniz.

Sin Cos Tan'ın tanımı

Trigonometrik değerler tablosuna girmeden önce, ilk olarak trigonometri ve sin cos tan terimlerini anlamamıza yardımcı olur.

Trigonometri , bir üçgenin uzunluğu ve açısı arasındaki ilişkiyi inceleyen bir matematik dalıdır.
Sin (sinüs) , açının önü ile hipotenüs, y / z arasındaki bir üçgendeki uzunluğun oranıdır.
Cos (kosinüs) , açının kenarı ile hipotenüs, x / z arasındaki bir üçgendeki uzunluğun oranıdır.
Tan (tanjant) , köşenin önü ile yan y / x arasındaki bir üçgendeki uzunlukların oranıdır.

Tüm bronz günah çünkü trigonometrik karşılaştırmalar yalnızca 90 derecelik bir açıya sahip dik üçgenler veya üçgenler için geçerlidir.

Çeyrek I Özel Açılı Trigonometri Tablosu (0-90 derece)

Köşe	0 º	30 º	45 º	60 º	90 º
Günah	0	1/2	1/2 √2	1/2 √3	1
Çünkü	1	1/2 √3	1/2 √2	1/2	0
Tan	0	1/2 √3	1	√3	∞

Özel Açı Çeyreği II (90-180 derece) Trigonometri Tablosu

Köşe	90 º	120 º	135 º	150 º	180 º
Günah	1	1/2 √3	1/2 √2	1/2	0
Çünkü	0	- 1/2	- 1/2 √2	- 1/2 √3	-1
Tan	∞	-√3	-1	- 1/3 √3	0

Sin Cos Tan Masa Özel Açı Çeyreği III (180-270 derece)

Köşe	180 º	210 º	225 º	240 º	270 º
Günah	0	- 1/2	- 1/2 √2	- 1 / 2√3	-1
Çünkü	-1	- 1 / 2√3	- 1 / 2√2	- 1/2	0
Tan	0	1 / 3√3	1	√3	∞

Cos Sin Tan Masa Özel Açı Çeyreği IV (270 - 360 derece)

Köşe	270 º	300 º	315 º	330 º	360 º
Günah	-1	-½√3	-½√2	-½	0
Çünkü	0	½	½√2	½√3	1
Tan	∞	-√3	-1	-1 / 3√3	0

Bu, 0 - 360 derece arasındaki tüm özel açılardan trigonometrik tabloların eksiksiz bir listesidir.

Ayrıca şunu okuyun: İnsan Görme Mekanizması Süreci ve Göz Sağlığı İpuçları

Bu tabloyu matematikte trigonometri hesaplama veya analiz etmede işi kolaylaştırmak için kullanabilirsiniz.

Özel Açılı Trigonometrik Tabloyu Ezberlemeden Hatırlama

Aslında, tüm trigonometrik değerleri her açıdan ezberlemek zorunda değilsiniz.

İhtiyacınız olan tek şey, belirli bir açının trigonometrik değerini bulmak için kullanabileceğiniz temel bir anlayış kavramıdır.

Üçgenin yan uzunluk bileşenlerini 0, 30, 45, 60 ve 90 derecelik özel açılarda hatırlamanız yeterlidir.

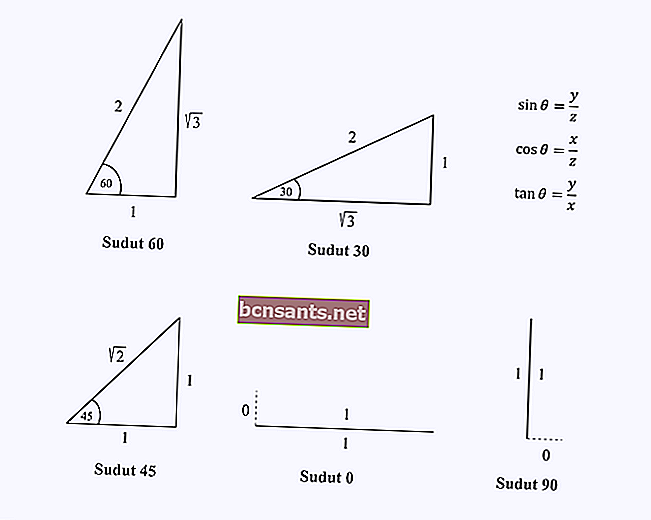
Cos (60) 'ın değerini bulmak istediğinizi varsayalım.

Sadece üçgenin kenar uzunluğunu 60 derecelik bir açı ile hatırlamanız, ardından o üçgen üzerinde x / z olan kosinüs işlemini gerçekleştirmeniz gerekir.

Şekilde cos 60 = 1/2 olduğunu göreceksiniz.

Kolay değil mi?

Diğer kadranlardaki açılar için yöntem aynıdır ve sadece her kadranın pozitif veya negatif işaretini ayarlamanız gerekir.

Daire Şeklinde Tablo

Yukarıdaki cos sin tan tablosu hatırlamak için çok uzunsa, ayrıca düşündüğünüz özel açı kavramı yöntemi hala zor ise ...

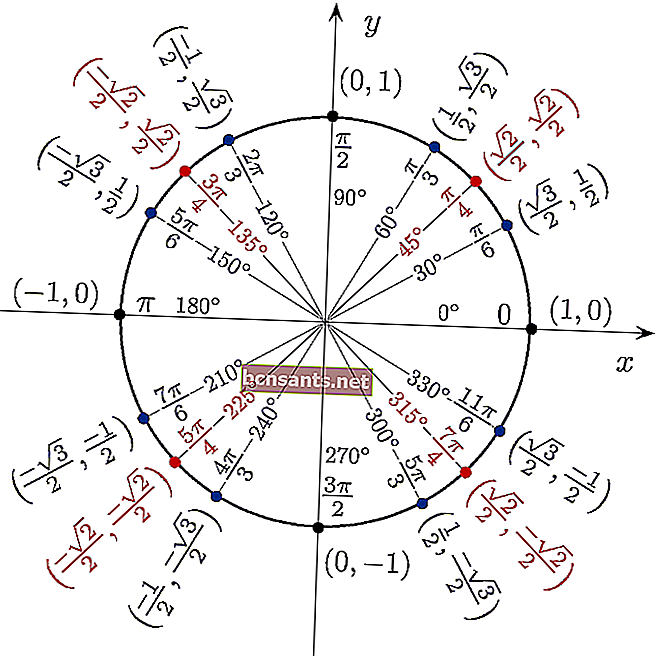
360 derecelik bir açıdan sin cos tan değerini doğrudan görmek için trigonometrik tabloyu daire şeklinde kullanabilirsiniz.

Trigonometrik Tabloları Ezberlemek İçin Hızlı Püf Noktaları

Yukarıdaki yöntemlere ek olarak, trigonometrik formül tablolarını kolayca hatırlamak için kullanabileceğiniz bir yöntem daha vardır.

Yapmanız gereken adımlar aşağıdaki gibidir:

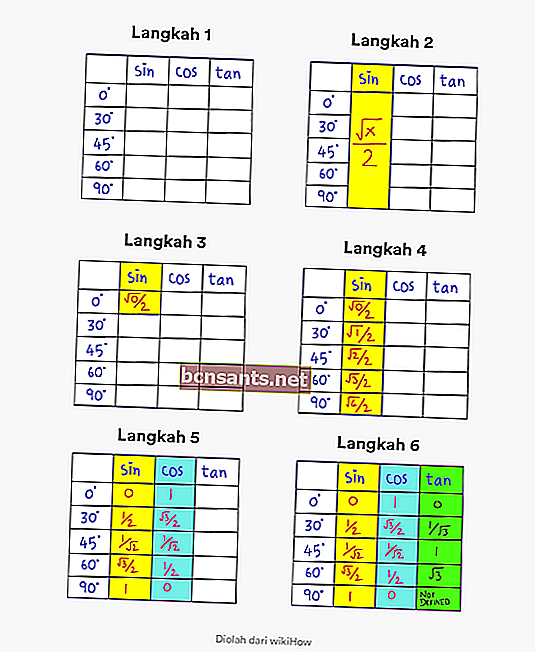
1. Adım . 0 - 90 derece açıları ve sin cos tan açıklamasına sahip sütunları içeren bir tablo oluşturun
2. Adım . 0 - 90 derecelik bir açıda günah için genel formülün √x / 2 olduğuna dikkat edin.
3. Adım . İlk sütunda √x / 2'de x değerini 0 olarak değiştirin. Sol üst köşe.
Adım 4. sin sütununda x'i 0, 1, 2, 3, 4 olarak değiştirerek sırayı doldurun. Böylece tam trigonometrik değere sahipsin.
5. Adım . Cos değerini bulmak için tek yapmanız gereken günah sütunundaki sırayı tersine çevirmektir.
6. adım . Bronzluk değerini bulmak için tek yapmanız gereken günah değerini cos değerine bölmektir.

Ayrıca şunu okuyun: Kurgusal Hikayeler: Örnekler, Tanımlar ve Öğeler [TAM

Trigonometrik tablo nasıl ezberlenir sin cos tan

Tan sin cos'un trigonometri değerini hatırlamak sizin için hangisi daha kolay?

Her iki durumda da, anlamanız en kolay olanı seçin. Çünkü her insanın farklı bir öğrenme stili vardır.

Tüm Açılardan Tablolar

Yukarıdaki tablolarda gösterilen değerler sadece özel açıların trigonometrik değerleri ise, bu tablo 0 - 90 derece arasındaki tüm açıların tüm trigonometrik değerlerini gösterir.

Köşe	Radyan	Günah	Çünkü	Tan
0 °	0	0	1	0
1 °	0,01746	0,01746	0.99985	0,01746
2 °	0,03492	0,03491	0.99939	0,03494
3 °	0,05238	0,05236	0.99863	0,05243
4 °	0.06984	0,06979	0.99756	0,06996
5 °	0.0873	0.08719	0.99619	0,08752
6 °	0.10476	0.10457	0.99452	0.10515
7 °	0.12222	0,12192	0.99254	0,12283
8 °	0.13968	0.13923	0.99026	0.1406
9 °	0.15714	0.1565	0.98768	0.15845
10 °	0.1746	0.17372	0.9848	0.1764
11 °	0,19206	0.19089	0.98161	0,19446
12 °	0.20952	0.20799	0.97813	0.21265
13 °	0.22698	0,22504	0.97435	0,23096
14 °	0.24444	0,24202	0.97027	0.24943
15 °	0,26191	0,25892	0.9659	0,26806
16 °	0.27937	0.27575	0.96123	0,28687
17 °	0,29683	0,29249	0.95627	0.30586
18 °	0,31429	0.30914	0.95102	0,32506
19 °	0,33175	0,32569	0.94548	0,34448
20 °	0.34921	0,34215	0.93965	0,36413
21 °	0,36667	0,35851	0.93353	0,38403
22 °	0,38413	0,37475	0.92713	0.40421
23 °	0.40159	0,39088	0.92044	0.42467
24 °	0,41905	0.40689	0.91348	0.44543
25 °	0,43651	0.42278	0.90623	0,46652
26 °	0,45397	0,43854	0.89871	0,48796
27 °	0,47143	0.45416	0.89092	0,50976
28 °	0.48889	0.46965	0.88286	0,53196
29 °	0,50635	0,48499	0.87452	0,55458
30 °	0.52381	0.50018	0.86592	0.57763
31 °	0,54127	0.51523	0.85706	0.60116
32 °	0,55873	0.53011	0.84793	0.62518
33 °	0.57619	0,54483	0.83854	0.64974
34 °	0,59365	0,55939	0.8289	0,67486
35 °	0.61111	0,57378	0.81901	0.70057
36 °	0.62857	0.58799	0.80887	0.72693
37 °	0,64603	0.60202	0.79848	0,75396
38 °	0.66349	0.61587	0.78785	0,78172
39 °	0.68095	0.62953	0.77697	0.81024
40 °	0.69841	0.643	0.76586	0.83958
41 °	0.71587	0.65628	0,75452	0.86979
42 °	0.73333	0.66935	0,74295	0.90094
43 °	0.75079	0,68222	0.73115	0.93308
44 °	0.76825	0,69488	0.71913	0.96629
45 °	0,78571	0.70733	0,70688	1.00063
46 °	0.80318	0.71956	0,69443	1.0362
47 °	0.82064	0,73158	0,68176	1.07308
48 °	0.8381	0,74337	0,66888	1.11137
49 °	0.85556	0,75494	0.6558	1.15117
50 °	0.87302	0.76627	0,64252	1.1926
51 °	0.89048	0.77737	0,62904	1.2358
52 °	0.90794	0.78824	0.61537	1.28091
53 °	0.9254	0,79886	0.60152	1.32807
54 °	0.94286	0.80924	0.58748	1.37748
55 °	0.96032	0.81937	0,57326	1.42932
56 °	0.97778	0.82926	0,55887	1.48382
57 °	0.99524	0,83889	0.5443	1.54122
58 °	1.0127	0.84826	0,52957	1.60179
59 °	1.03016	0.85738	0.51468	1.66584
60 °	1.04762	0.86624	0,49964	1.73374
61 °	1.06508	0.87483	0,48444	1.80587
62 °	1.08254	0.88315	0,46909	1.8827
63 °	1.1	0.89121	0,4536	1.96476
64 °	1.11746	0.89899	0,43797	2.05265
65 °	1.13492	0.9065	0.4222	2.14707
66 °	1.15238	0.91373	0.40631	2.24884
67 °	1.16984	0.92069	0,3903	2.35894
68 °	1.1873	0.92736	0,37416	2.4785
69 °	1.20476	0.93375	0,35792	2.60887
70 °	1.22222	0.93986	0,34156	2.75169
71 °	1.23968	0.94568	0.3251	2.90892
72 °	1.25714	0.95121	0.30854	3.08299
73 °	1.2746	0.95646	0,29188	3.27686
74 °	1.29206	0.96141	0.27514	3.49427
75 °	1.30952	0.96606	0,25831	3.73993
76 °	1.32698	0.97043	0.2414	4.01992
77 °	1.34444	0.97449	0.22442	4.34219
78 °	1.36191	0.97826	0.20738	4.71734
79 °	1.37937	0.98173	0.19026	5,15984
80 °	1.39683	0.98491	0.1731	5,68998
81 °	1.41429	0.98778	0.15587	6,33709
82 °	1.43175	0.99035	0.1386	7.14523
83 °	1.44921	0.99262	0,12129	8.18379
84 °	1.46667	0.99458	0.10394	9.56868
85 °	1.48413	0.99625	0,08656	11.5092
86 °	1.50159	0.99761	0,06915	14.4259
87 °	1.51905	0.99866	0,05173	19.3069
88 °	1.53651	0.99941	0,03428	29.153
89 °	1.55397	0.99986	0,01683	59.4189
90 °	1.57143	1	0	∞

Umarım bu trigonometrik açıklama sizin için yararlı olabilir.

Bu materyal, ileri matematik ve fizikteki çeşitli uygulamalar için çok faydalı olacaktır.

Ayrıca Saintif'te asal sayılar, birim dönüştürme, dikdörtgen formüller vb. Gibi diğer okul materyallerini de öğrenebilirsiniz.

Referans

Trigonometri - Wikipedia
Matematik Araçları - Trigonometri