
Analizdeki mutlak değer, hem denklemlerde hem de eşitsizliklerde çeşitli matematik problemlerini çözmek için çok kullanışlıdır. Aşağıda, mutlak değerlerin tam bir açıklaması ve örnek sorular yer almaktadır.
Mutlak Değerin Tanımı
Tüm sayıların kendi mutlak değerleri vardır. Tüm mutlak sayılar pozitiftir, bu nedenle aynı sayıya sahip sayıların mutlak sayı değerleri ancak pozitif (+) ve negatif (-) gösterimler arasındaki fark aynı mutlak sayı sonucuna sahip olacaktır.
Eğer x bir gerçek sayının üyesiyse, mutlak değer | x | olarak yazılır. ve aşağıdaki gibi tanımlanır:

"Mutlak değer, koordinatlarda başlangıç veya sıfır noktasından aynı uzunluk veya uzaklık değerine sahip bir sayıdır."
5'in mutlak değerinin, 0 noktasından 5 noktasına veya (-5) noktasına kadar uzunluk veya mesafe olduğu yorumlanabilir.
(-9) ve 9'un mutlak değerleri 9'dur. 0'ın mutlak değerleri 0'dır, vb. Nilaa
Aşağıdaki resme bakarak kesinlikle anlayacağım:

Yukarıdaki resimde | 5 | değerinin olduğu anlaşılmaktadır. 5 noktasının 0 rakamına olan uzaklığı, yani 5 ve | -5 | (-5) noktasının 0 sayısından uzaklığı 5'tir.
Eğer | x | x noktasından 0'a, sonra | xa | x noktasından a noktasına olan mesafedir. Örneğin 5. noktadan 2. noktaya olan mesafeyi ifade ederken | 5-2 | = 3 şeklinde yazılabilir.

Genel olarak x'in a'ya uzaklığının | xa | notasyonu ile yazılabileceği söylenebilir. veya | balta |
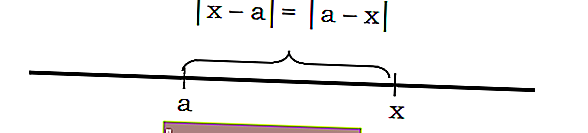
Örneğin, bir sayının 3. noktaya olan mesafesi aşağıdaki gibi 7 değerindedir:
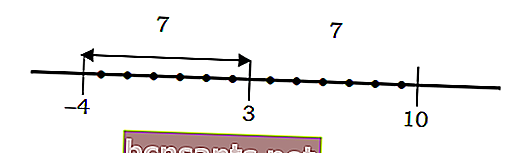
Cebirsel denklemde tanımlanmışsa | x-3 | = 7 aşağıdaki gibi çözülebilir:
Ayrıca şunu okuyun: Logaritmalarla Depremleri Ölçme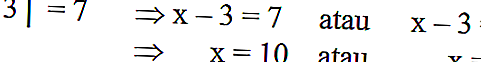
Unutmayın ki | x-3 | | x-3 | = 7, x sayısının 7 birim boyunca nokta 3'e olan mesafesidir.
Mutlak Değerin Özellikleri
Mutlak sayı denklem işlemlerinde, mutlak sayı denklemlerini çözmeye yardımcı olabilecek mutlak sayı özellikleri vardır.
Mutlak değer denklemlerinde genel olarak mutlak sayıların özellikleri aşağıdadır:

Eşitsizliğin mutlak değerinin özellikleri:
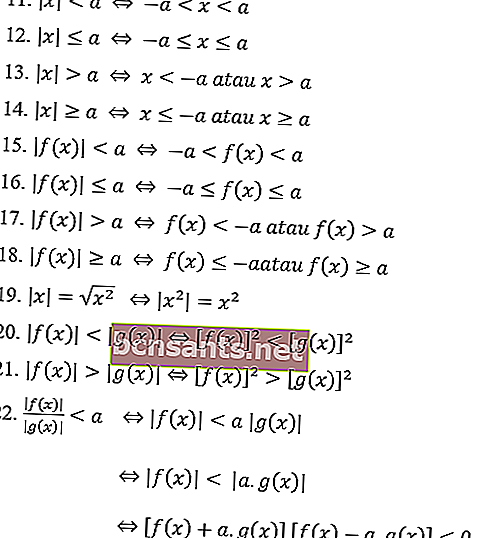
Mutlak Değer Denklem Problemlerine Örnekler
Örnek Problem 1
| 10-3 | denkleminin mutlak değeri nedir?
Cevap:
| 10-3 | = | 7 | = 7
Örnek Problem 2
| X-6 | = 10 mutlak değerinin denklemi için x'in sonucu nedir?
Cevap:
Bu denklemi çözmek için, mutlak sayılar için iki olası sonuç vardır.
| x-6 | = 10
İlk çözüm:
x-6 = 10
x = 16
ikinci çözüm:
x - 6 = -10
x = -4
Yani bu denklemin cevabı 16 veya (-4)
Örnek Problem 3
Aşağıdaki denklemde x değerini çözün ve hesaplayın
–3 | x - 7 | + 2 = -13
Cevap:
–3 | x - 7 | + 2 = -13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| x - 7 | = –15 / –3
| x - 7 | = 5
Yukarıdaki çözüme kadar yapılırsa, x değerinin iki değeri olur
x - 7 = 5
x = 12
veya
x - 7 = - 5
x = 2
yani son x değeri 12 veya 2'dir
Örnek Problem 4
Aşağıdaki denklemi ve x değerinin ne olduğunu çözün
| 7 - 2x | - 11 = 14
Cevap:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
Yukarıdaki denklemi tamamladıktan sonra, x'in mutlak değeri için sayılar aşağıdaki gibidir
7 - 2x = 25
2x = - 18
x = - 9
veya
7 - 2x = - 25
2x = 32
x = 16
Dolayısıyla son x değeri (- 9) veya 16'dır
Örnek Problem 5
Aşağıdaki mutlak değer denkleminin çözümünü bulun:
| 4x - 2 | = | x + 7 |
Cevap:
Yukarıdaki denklemi çözmek için iki olası çözümü kullanın, yani:
Ayrıca şunu okuyun: Adaylar için seçilebilirlik anketi istatistiklerinin sonuçlarını okurken hatalar4x - 2 = x + 7
x = 3
veya
4x - 2 = - (x + 7)
x = - 1
Denklemin çözümü | 4x - 2 | = | x + 7 | x = 3 veya x = - 1
Örnek Problem 6
Aşağıdaki mutlak değer denkleminin çözümünü belirleyin:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
x değeri nedir?
Cevap:
Basitleştirme: | 3x + 2 | = p
sonra
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(p + 2) (p - 1) = 0
p + 2 = 0
p = - 2 (mutlak değer negatif değildir)
veya
p - 1 = 0
p = 1
| 3x + 2 | = 1
Yukarıdaki çözüme kadar, x için 2 olası cevap vardır:
3x + 2 = 1
3x = 1-2
3x = - 1
x = - 1/3
veya
- (3x + 2) = 1
3x + 2 = - 1
3x = - 1-2
3x = - 3
x = - 1
Yani denklemin çözümü x = - 1/3 veya x = - 1
Referans: Mutlak Değer - Matematik Eğlencelidir
