
Belirsiz integral veya aynı zamanda anti-türev olarak da bilinir, yeni bir fonksiyon üreten bir entegrasyon işlemi biçimidir .
İntegral, matematikte çok önemli bir rol oynar. Teori, bir fonksiyonun eğrisinin altındaki alanı belirleyebilir.
İntegral, sürekli bir fonksiyon üzerinde sürekli olan toplam limiti için kullanışlıdır. İntegral, anti-türevdir. Daha sonra, f sürekli bir fonksiyonsa, f fonksiyonunun integral sonucu F olarak gösterilir.
Belirli işlevsel sınırlara dayanan intergral tipler kesin değildir. Aşağıda, sınırsız limitli integral türleri için bir tartışma yer almaktadır.
Belirsiz İntegral
Belirsiz bir integral veya aynı zamanda anti-türev veya anti-dalgalanma olarak da bilinen, yeni bir fonksiyon üreten bir entegrasyon işlemi biçimidir.
Aşağıdaki denklemi düşünün.

C sabit ile. Belirsiz integral formülü aşağıdaki gibidir
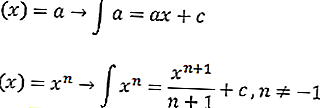
veya eşittir

ile
- a (x) ^ n = Denklem işlevi
- a = Sabit
- x = Değişken
- n = Denklem fonksiyonunun gücü
- C = sabit
Bu belirsiz integralin sonucu, yeni fonksiyonda hala değişkenler olduğu için belirli veya belirli bir değeri olmayan yeni bir fonksiyon olan fonksiyondur.
Belirsiz integral kavramını daha iyi anlayabilmeniz için aşağıdaki örnek problemi düşünün.

Bu örneğe dayanarak, bir integral işlem formüle edilebilir, yani
Trigonometrik İntegral
Bir fonksiyonun integrali mutlaka sabit, doğrusal veya polinom değildir. Bu galaksiler arası çözümde, genellikle trigonometrik öğeler içerir.
Trigonomik fonksiyonda, aşağıdaki tabloda düzenlenen integrallerin tanımları da geçerlidir.
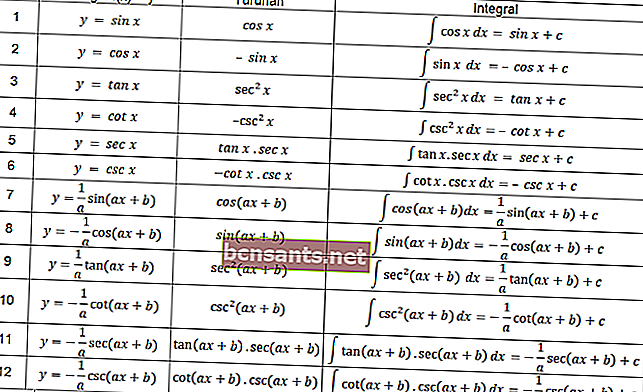
Trigonometri içeren integral problemini çözmek için yukarıdaki tablodaki denklemleri kullanabilirsiniz.
Trigonometrik integralleri daha iyi anlamak için aşağıdaki örnekleri anlayabilirsiniz
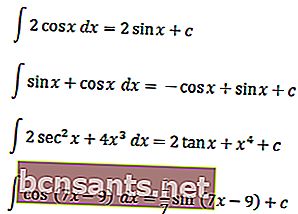
Sıradan ve özel trigonometrik fonksiyonlardaki belirsiz integrallerin açıklaması buydu. Umarım iyi incelenebilir.
Ayrıca şunu okuyun: Ahlak normları: Tanım, Amaç, Yaptırımlar ve Örnekler [TAM]Bu integralin kavramını daha iyi anlamak için alıştırma soruları yapma alıştırması yapabilirsiniz. Sormak istediğiniz bir şey varsa, bunu yorumlar sütununa yazın.
